Previous: A Geometric Series Problem with Shifting Indicies
Next: Videos on the Introduction to Infinite Series
Problem
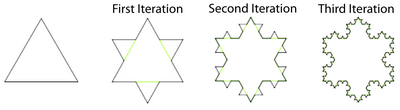
Suppose we would like to calculate the area of the "Koch Snowflake". The Koch Snowflake is an object that can be created from the union of infinitely many equilateral triangles (see figure below).
We construct the Koch Snowflake in an iterative process. Starting with an equilateral triangle, each iteration consists of altering each line segment as follows:
- divide the line segment into three segments of equal length
- draw an equilateral triangle that has the middle segment from step 1 as its base and points outward
- remove the line segment that is the base of the triangle from step 2
The Koch Snowflake is the limit approached as the number of iterations goes to infinity.
Solution
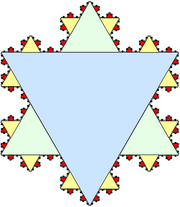
Now, to derive an expression for the area of our construction at the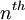 
iteration, let's start with the fifth iteration. The fifth iteration of the snowflake is shown below, with its iterations in different colours.
Blue and Green Triangles
Assume that the one blue triangle as unit area. Each side of the green triangle is exactly 1/3 the length of a side of the blue triangle, and therefore has exactly 1/9 the area of the blue triangle. There are three green triangles, so the green and blue triangles have an area of
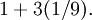
Blue, Green, and Yellow Triangles
Each of the 12 = 3•4 yellow triangles has 1/9 the area of a green triangle, or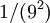 
the area of a blue triangle. The area of the blue, green, and yellow triangles is
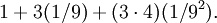
Blue, Green, Yellow, and Red Triangles
Each of the 48 = 3•4•4 red triangles has 1/9 the area of a yellow triangles, or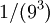 
the area of a blue triangle. The area of the blue, green, yellow, and red triangles is
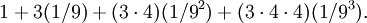
Total Area
The total area of the snowflake uses the infinite sequence
.
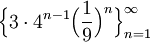We will add all the terms of the series together, and add 1, to produce the following sum
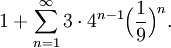
Seeing that this is a geometric series with a = 1/3 and r = 4/9, we immediately conclude that this series converges and is equal to
Previous: A Geometric Series Problem with Shifting Indicies
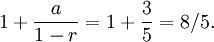
Next: Videos on the Introduction to Infinite Series
This is all wrong. The number of yellow triangles is 12 not 9, and that makes the infinite sequence wrong as well.
“each yellow triangle has 1/9 the area of a green triangle, or 1/27 the area of a blue triangle. ” But if a yellow triangle is 1/9 of a green triangle which is in turn 1/9 of a blue triangle, wouldn’t that make a yellow triangle equivalent to 1/81 of a blue triangle? Also- you say “The area of the blue, green, and yellow triangles is 1 + 3(1 / 9) + 9(1 / 27) = 5 / 3.”, you multiply 1/27 by 9 when it should be multiplied by 12 because there are 12 yellow triangles. Am I just really confused or is your math all wrong?
This is wrong!
The r = 4/9 not 1/9.