[previous] [next]
Problem
Find the sum of the series
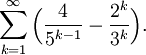
Complete Solution
We can break this problem down into parts and apply the theorem for convergent series to combine each part together.
Step (1): Find the Sum of the First Term
The first term in the problem is a geometric series that can be simplified:
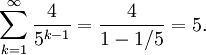
Step (2): Find the Sum of the Second Term

Step (3): Combining Results
Combining results from Steps (1) and (2) yields
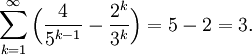
Discussion of Each Step
Step (1)
The infinite series
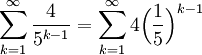
is a geometric series with common ratio 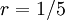 and first term
and first term 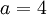 . Therefore, we can apply our formula
. Therefore, we can apply our formula
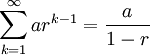
for computing the sum of a geometric series.
Step (2.1)
The infinite series is geometric, and so we can find its sum by working it into the the form
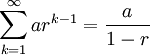
to apply our summation formula. One way of starting this process is to making the exponent equal to 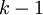 , which we carried out by shifting the summation index up by one (other approaches may be used, see discussion below in the Possible Challenges section).
, which we carried out by shifting the summation index up by one (other approaches may be used, see discussion below in the Possible Challenges section).
Step (2.2)
The index of summation can be shifted down to 1, requiring that we subtract 1. This process was described in the lecture on sigma notation.
Steps (2.3) and (2.4)
Now that our geometric series in the needed form to apply our summation formula, we may equate our series to
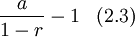
and substitute our values of 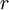 and
and 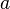 to obtain Step (2.4).
to obtain Step (2.4).
The rest of Step (2) is algebraic manipulation (fractions).
Step (3)
Because we have found two convergent infinite series, we can invoke the fourth property of convergent series (the sum of two convergent series is a convergent series) to compute the sum of the given problem:
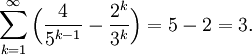
For demonstration purposes, more steps were shown than what students may find that are needed to solve problems during assessments.
Possible Challenge Areas
Converting the Series Into the Needed Form
Students completing this problem may have noticed that our geometric series formula
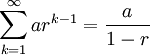
can only be applied when the summation starts at 1 and the exponent is 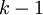 . In simplifying the second term, we needed to convert our problem into this form, which could be solved in another way. Another way of making the conversion is as follows:
. In simplifying the second term, we needed to convert our problem into this form, which could be solved in another way. Another way of making the conversion is as follows:

Yet even more methods of finding the sum of this series could be used. While we have applied the formula
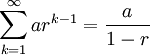
some calculus textbooks introduced the equivalent formula
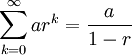
which leads to other similar approaches to finding the sum of the infinite series.
[previous] [next]


it should be 5-2 not 5+2
Thank you. I’ve fixed the error.