Introduction: Telescoping and Harmonic Series

Recall that our definition of a convergence of an infinite series

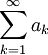
was given by the following: if the limit

exists, then the given series is convergent. Otherwise, it is divergent.

We used this definition to study one particular infinite series, the geometric series, whose general form is

A reasonable question to ask would be: can we use the definition of convergence to explore the convergence of other special forms?

Two Special Forms: The Telescoping and Harmonic Series

Suppose we are asked to determine if the series

or

converge. Clearly, these are not geometric series. How could we determine if they converge? Where would we begin to answer such a question?

Our convergence definition can actually be applied directly to study these two series. In the first series, we can show that it is divergent. In the second series, we can use the definition to show that it converges and find its sum.

No Proofs

This lesson does not include any theory or proofs. For our purposes, it will be sufficient to demonstrate these two special forms with a set of examples.