The Harmonic Series

Another useful example of a series whose convergence we can determine based on the behaviour of the partial sums is the harmonic series, whose infinite sum is given by

Do you think this infinite series converges? The terms of the sequence are monotonically decreasing, so one might guess that the partial sums would in fact converge to some finite value and hence the sequence would converge.

Plotting the Partial Sums of the Harmonic Series

The widget below plots the partial sums of the harmonic series for a chosen n. That is, it plots

for a value of n that you provide. Does it look like the partials sums are converging?

Convergence of the Harmonic Series

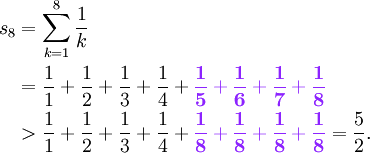
There are a few different ways to to determine whether the harmonic series converges, but we will investigate this question using the definition of convergence above. Let's look at a few of the partial sums, and see if we can find a pattern. For and 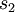we have

Moving ahead to 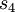we find (using highlighting to bring attention to what changes are made to create our inequality)

We are beginning to see a pattern now. If we work ahead to , we obtain

Hence, it can be shown that in general,

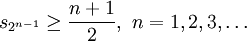
As 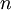tends to infinity, the partial sums go to infinity. Hence, using the definition of convergence of an infinite series, the harmonic series is divergent.

Alternate proofs of this result can be found in most introductory calculus textbooks, which the reader may find helpful. In any case, it is the result that students will be tested on, not its derivation.