Maclaurin Expansion of ex

Previous: The Taylor Series

Next: Maclaurin Expansion of sin(x)




Example

Find the Taylor series expansion for ex when x is zero, and determine its radius of convergence.

Complete Solution

Before starting this problem, note that the Taylor series expansion of any function about the point c = 0 is the same as finding its Maclaurin series expansion.

Step 1: Find Coefficients

Let f(x) = ex. To find the Maclaurin series coefficients, we must evaluate

for k = 0, 1, 2, 3, 4, ....

Because f(x) = ex, then all derivatives of f(x) at x = 0 are equal to 1. Therefore, all coefficients of the series are equal to 1.

Step 2: Substitute Coefficients into Expansion

By substitution, the Maclaurin series for ex is

Step 3: Radius of Convergence

The ratio test gives us:

Because this limit is zero for all real values of x, the radius of convergence of the expansion is the set of all real numbers.

Explanation of Each Step

Step 1

Maclaurin series coefficients, ak are always calculated using the formula

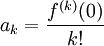
where f is the given function, and in this case is e(x). In step 1, we are only using this formula to calculate coefficients. We found that all of them have the same value, and that value is one.

Step 2

Step 2 was a simple substitution of our coefficients into the expression of the Taylor series given on the previous page.

Step 3

This step was nothing more than substitution of our formula into the formula for the ratio test. Because we found that the series converges for all x, we did not need to test the endpoints of our interval. If however we did find that the series only converged on an interval with a finite width, then we may need to take extra steps to determine the convergence at the boundary points of the interval.

Possible Challenges

What are we Doing?

The following video provides a graphical interpretation of the Taylor approximation to ex about the point c = 3. In the derivation above, we considered an expansion at c = 0. The instructor uses the term "Taylor approximation" in the same way we use the term "Taylor expansion".

Visualizing Taylor Series for e^x
A graphical description of the Taylor series of ex.
This video can be found on the Kahn Academy website, and carries a Creative Commons copyright (CC BY-NC-SA 3.0).

Summary

In this example, we found the Macluarin expansion of the exponential function.

The Maclaurin Expansion of ex
The Maclaurin series expansion for ex is given by

This formula is valid for all real values of x.


Previous: The Taylor Series

Next: Maclaurin Expansion of sin(x)




1 Response to Maclaurin Expansion of ex

  1. Cydney Brook says:
    2021-03-11 at 10:34

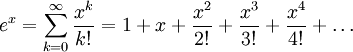
    Visualizing Taylor polynomial approximations is a good way to do some basic homework for students in higher mathematics. Before we get started, though, let’s make sure that you understand the concept behind Taylor polynomial equations. Taylor polynomials are formulas where the output value will depend on the input variable selected by the student. For example, the output value for the quadratic equation y = a * b can be either zero or infinity depending upon whether it is positive or negative. So we have the Taylor polynomial equations y = (a * b) + (c * d) where c and d are constants. This can also be written as y = (a * sin (b * sin (c * sin (d * sin(a)), where a and d are constant).

Leave a Reply