When considering a challenging science concept, I recalled struggling with explaining the concept of floatation, or “sink or float”, when teaching kindergarten. Although exploring objects that sink and float in water is highly intriguing for young students, the reasoning behind which objects sink and float can get complicated and too abstract for a student at that age to fully understand. Why does a tiny popcorn kernel sink and a large watermelon float?
In the BC’s New Science Curriculum, density is not specifically addressed until grade six when students investigate heterogenous mixtures. In Suat Unal’s (2008) research, he recognizes that elementary students possess significant misconceptions relating to floatation as evidenced through other research by Biddulph and Osborne (1984) and Gürdal and Macaroglu (1997). This other research finds that “students offered many unrelated factors such as mass and weight” to explain floatation activity, and that even after sink and float investigations and learning of Archimedes had been completed, students “were unable to construct scientific understanding” about sink and float relations (p.135).
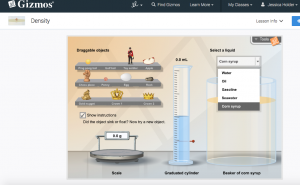
In preparing a T-GEM lesson, I wanted to include student investigation of objects that sink and float in water, as well as in other liquids, to help student understanding of the concept of density. Because of this specification, the Gizmos simulation that is included in the following lesson is ideal, whereas other simulations that I found online provide investigation solely with water. An image of the simulation follows:
T-GEM Lesson – Density – Grade 6 (BC Curriculum)
| Teaching Strategies | Student Activity | |
| Read Aloud – Chapter 5, “Archimedes and King Hiero’s Crown” from Archimedes and the Door of Science by Jeanne Bendick. | Class discussion narrating ideas presented through reading; teacher comments neutrally | |
|
GEM – Cycle 1 |
||
| G – Generate | Instruct students to investigate selected object in a sink and float investigation using water in a container. Students are to record observations on a T-chart as well as represent observations on a paper chart template using cut and paste images of the selected objects. Ask students to make a prediction about the types of objects that sink vs. float. | With a partner, students test sink and float tendencies of selected objects in water and record on a T-chart; Students place cut out pictures of objects onto chart template; After recording data, student journal predictions about the types of objects that sink vs. float. |
| E – Evaluate | Ask students to record anything that does not make sense about their observations and prediction – questions they may have or confusing patterns; Ask students to think of a way to conduct a sink and float investigation that could help clarify some of the observations and predictions that do not make sense. Prompt students with a change in variable – either the solid objects or the liquid. Teacher guides student through extension investigations using an alternate liquid. | Students discuss with partner and record observations and predictions that don’t makes sense; Share questions and confusing patterns with class and plan a new investigation with changing one variable. Watch teacher directed demonstration and participate in class discussion. |
| M- Modify | Ask students to determine what changes they need to add to their T-chart and paper pictorial chart to accommodate the new information accessed from the teacher-led investigation | Student makes adjustments to representations of t-chart and paper pictorial chart by including results with variable change. |
|
T-GEM – Cycle 2 |
||
| G- Generate | Direct students to Gizmos online simulations: https://www.explorelearning.com {Teacher needs to previously set up an account and select simulation to add to their “class”.}
Lead students to the the elementary level lesson under Physics called “Density” Provide a short explanation of the activity, sharing that instructions are provided in text within the simulation. Remind students to record on a new chart the weight (g) of the object when measured on the scale, the volume displacement (mL)of the object within the graduated cylinder, and the the ability of the object to sink and float in each of the available liquids (water, oil, gasoline, sea water and corn syrup). After all objects have been tested, journal a relation statement based on the acquired data. |
In partners, students use the Density simulation measuring weight and volume displacement of the following objects: ping pong ball, golf ball, toy soldier, apple, chess piece, penny, egg, rock, gold nugget, crown 1 and crown 2. Students will test the floatation of each object in five different liquids and record their observations. Students will analyze their data and make a relation statement in their journal. |
| E-Evaluate | Teacher provides students with the equation for density:
Density = Mass/Volume Water = 1.00 g/mL Oil = 0.92 g/mL Gasoline = 0.70 g/mL Sea Water = 1.03 g/mL Syrup = 1.33 g/mL |
Students compare the density of the measured objects using the density equation and with the density of the liquids and evaluate their relation statement making changes as necessary. |
| M-Modify | Ask students to design a pictorial representation (model) of the data. Students can choose to represent objects that sink, or float, or both. The model should include density measurements of both the liquids and objects. The model should include a comparison of two or more liquids. Recommend using a chart or graph format with pictorial representations of objects. | Students choose data to include in their model representation following criteria provided by teacher. |
Hi Jessica,
Really great and detailed T-GEM cycle. When I previously taught Science 8, the concept of density was part of the course. I could definitely see the benefits of using the simulation to assist in understanding the concept of floating and sinking (we do a practical lab similar to the simulation). However, I wonder if at Grade 8 (or even Grade 6) if students themselves are able to find the relationship or even a correlation between mass, volume and density. The simulation seems to provide data on the three variables but not the definitive relationship. I would be keen to see if students would be able to develop that relationship on their own instead of being provided the formula outright. Nonetheless, thanks for the post and giving me something to think about the next time I teach Grade 8!
Hi Darren,
As I was working through designing the GEM lesson, I realized that the information for the relationship between density, mass and volume needed to be given to the students. Direct teacher instruction can be a component of GEM as promoted by the chemistry teacher in the Khan studies (2007) and (2011) in this past week’s required readings. In the second GEM cycle, the teacher activity includes direct instruction of the density formula and the density measurements of the five liquids tested in the simulation. I wonder if this is enough or if you think this would still be challenging for middle school students.
My apologies, Darren, I misread your comment about students developing a relation first, before providing the formula. I did assume in my lesson that this would be too challenging, but both you and Mary commented about this, so I will reevaluate 😉 that aspect of my lesson …
Thanks for your insights!
Hi Jessica,
I have used this Gizmo in my class when I was teaching grade 8 Science in Montreal! I thought you did an excellent job breaking down the T-GEM cycle. By having the students present their information in graph form you are also testing those skills. Thank you for this.
Haneefa
Thank you, Haneefa. I signed up for a 30 day trial to Gizmos and would like to explore more the simulations related to elementary science. I was impressed, and like I mentioned in my post, Gizmos seemed to take the testing to a further level than other similar simulations from other sites.
Our Board has decided that Gizmo’s are an excellent resource and have provided us all with a Board login to access whenever we need them. I have found that some of them are excellent, but others do not fit my purpose as well, so you need to make sure to check them out carefully before assigning them to the students. However, many of them are great.
Anne
Hi Jessica,
I really enjoyed your post and the ways you integrated the T-GEM model into your teaching of density. I appreciated that you included a variety of activities in your lesson to allow students with varying learning styles to access the information. I thought you also did a great job of showing the cyclical pattern of GEM that Khan discussed in her articles by having students engage in two GEM cycles within your lesson. I have never used the Gizmos program or simulations before, but I will definitely take a look at it now. Thank you for including a screenshot with your post – I am a very visual learner, so by including the image, you have increased my interest in the program as well as given me a clear understanding of what the interactive simulation looks like. I do wonder, along with Darren, if it might be possible to set the cycle up so that students are given the opportunity to come up with a relationship between mass, volume, and density before they are given the equation. I would expect that some students would not, but it could be a great challenge for students who tend to “exceed expectations” and who look for additional challenges.
Thanks, Mary, for your comment.
I misread Darren’s response regarding students developing a relationship prior to being given the equation. I was assuming that it would be too difficult for grade 6, but perhaps given a calculator, the students could figure out a relation…?? I am reevaluating that aspect of my lesson. Thank you for your encouraging and insightful words.
To be honest, I would be surprised if they could recreate the actual equation on their own (although maybe I am not giving students enough credit?), but it would be interesting to see what relationships they could come up with on their own and then perhaps you could use that to “create” the equation together as a class? Might be neat to experiment with?
I agree with many of the comments above, so will not reiterate them, however, one of the aspects I enjoyed about your lesson plan is the read aloud you are using as an introduction. I love it when there are picture books that help introduce the concepts and give the students another way to access some of the information. I use read alouds like this with my intermediate students as well and they always really enjoy story time. I think we do not do this enough with the older grades.
Anne
Hi Jessica,
Thank you for contributing a detailed T-GEM plan. It was informed by research on student conceptions such as, “students offered many unrelated factors such as mass and weight” to explain flotation. For your grade 6 class, you designed a TELE that involved a simulation and identified an affordance of this technology for your age group and curriculum: “I wanted to include student investigation of objects that sink and float in water, as well as in other liquids, to help student understanding of the concept of density.”
The T-GEM was a number of critical manouevers towards conceptual development. For example, reading, art, charts, scans, concept mapping, drawing, surveys, mini-quizzes are all ways to elicit prior ideas in math/science. Notable also in your plan is that teachers’ comments are neutral at the outset; there are no attempt to over-write student conceptions but rather to begin a process of questions to elicit how the grade 6 children think about this topic. The cyclical nature of GEM was also evident with 2 GEM cycles. This is an important component of GEM. (Sometimes the G is followed by E and M and then another cycle of E and M). There was also additional nuance: Direct teacher instruction can be a component of GEM as promoted by the chemistry teacher in the Khan studies (2007) and (2011) in this past week’s required readings.
A few ideas for elaboration: in the generation phase, it might be possible for students to ask each other questions based on their T charts, for example why did that object float float? In the Evaluation phase: given the selected objects, which ones are anticipated that won’t make sense to the students? Using anomalies in the way that I think you have developed is a potentially very powerful method. Clark Chinn writes more about this in his famous paper: Chinn, C. A., & Brewer, W. F. (1993). The role of anomalous data in knowledge acquisition: A theoretical framework and implications for science instruction. Review of educational research, 63(1), 1-49, and it was a method suggested in the case study an the Private Universe. In the Private Universe, when students suggest that the Earth is closer to the sun in summer as an explanation for the season, an anomalous piece of information is that the earth is actually closer to the Sun on Jan 04 than July 04.
It is worthwhile noting that there is an opportunity at multiple points for students to make a relation statement (in their journal). Making these relationship statements helps them to generate rules that can later be reconsidered, extended, or enriched beyond the case that they were originally applied to. These relationships may be qualitative, semi-quantitative (as X increases, Y decreases), or quantitative (equations, formulas).
In the modification phase, asking students to design a pictorial representation (model) of the data is one way to begin to inspect their conceptual understanding. it will be interesting to see how students represent heaver objects in these pictorial models. It would be very interesting to attempt to set the cycle up so that students are given the opportunity to come up with a relationship between mass, volume, and density before they are given the equation, as suggested by Darren and others. It would also serve to include the mathematics in the sciences or the science in the mathematics, consonant with STEM.
We look forward to hearing how your lesson went. Thank you, Samia