Mathematics
Targeted Group: Grade 7
Format: Number Sense and Numeration – Adding Fractions
Misconception: Adding fractions without finding common denominators or equivalent fractions.
Rationale:
Students have a great deal of difficulty with fractions and understanding why they need a common denominator in order to add them. As this seems to be an issue each year with grade 7 students I thought it would be a good idea to find new ways to address the concept.
Goals:
Students will be able to add fractions competently with like and unlike denominators, finding equivalent fractions in authentic problems.
Materials: Virtual fraction manipulatives
http://www.mhhe.com/math/ltbmath/bennett_nelson8e/VMK.html?initManip=fractionBars
Smartboard notebook software – Specific lesson plans
Authentic addition of fractions questions.
Process: This can be done individually or in pairs.
Step 1:
Give students a step by step adding fractions task sheet with three different tasks. The step by step process allows the students to see how the common denominator is found and how to add the fractions.
Step 2:
Direct students to the virtual manipulatives at the above URL. This would be in their Edmodo folder already so they just have to click on the link.
Step 3:
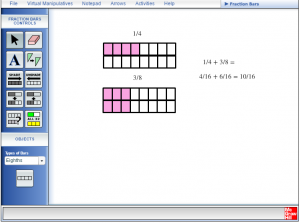
Direct students to create the model shown on the task sheet on the virtual page using fraction blocks. Students should write the addition statements on the virtual page, and then transfer them to their task sheet. They should continue to do this for all the questions on the task sheet.
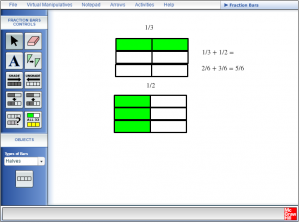
Step 5:
Ask the students to create their own addition problem using the fraction bars for the other students in the class to try. Students should be sure to draw this on their task sheet including the correct addition statements.
Consolidation Activity: Smartboard Notebook Lesson
Task:
Introduce students to the Land Ownership task. Show them the picture of the land split into various areas for different owners in SmartNotebook. Students can use this software on the laptop computers using the mouse.
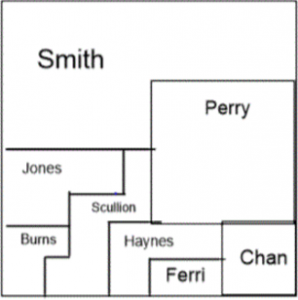
Work with a partner.
The map shows land owned by 8 families.
Determine what fraction of the land each family owns.
Four families sold land to the other four families.
Use the first map clues to help you draw the new map. You can use the back of the sheet to do this.
Write the addition to show each of the transactions.
CLUES
- When all the sales were finished, four families owned all the land – Smith, Perry, Haynes, and Chan.
- Each owner can walk on their land without having to cross another person’s property.
- Smith now owns 1/2 the land.
- Perry kept 1/2 of her land and sold the other half to Chan.
- Haynes bought land from two other people. He now owns 3/16 of the land.
- Chan now owns the same amount of land as Haynes.
Students use the tools in SmartNotebook to colour in the areas owned by each family and manipulate the shapes to find the smallest piece in order to determine the common denominator. Once they have done this, students find the equivalent fractions for each of the owners property showing the fraction in equivalent form and simplest form. For example: Perry = 1/4 or 16/64.
When they have found all the equivalent fractions it should be easier for them to rearrange the fractions for the four families to own all the land according to the clues. They need to show the new configuration on their screen or paper, and show the addition statements that go with their solutions.
Education Theories:
The educational theories that are associated with this lesson plan are Learning for Use and Anchored Instruction.
Learning for Use framework is a pedagogical framework that integrates the content with the processes of the subject matter. Using the virtual manipulatives allows the students to visualize the process of creating the equivalent fractions, how a common denominator is determined, and then how the two fractions are added together. Since the content is being able to add fractions with unlike denominators, the manipulatives allow the students to try a lot of different combinations of fractions to find their equivalents and add them. The virtual manipulatives also allow the students to discover these concepts for themselves, and build upon that understanding using the tiles to create a number of different combinations.
Anchored instruction is the process of presenting instruction in the context of an authentic environment with problems or issues which learners must resolve. The problems or issues which are presented to learners in the authentic environment are “anchors” which link learning of content and skills to authentic tasks and activities in which the learning must be used (Gittens, Thompson, & Carter). Although this is not a true representation of anchored instruction, the concept of buying and selling parcels of land is a real world connection. It is difficult to find authentic problems using fractions that the students would recognize. This problem could be related to their history or geography lessons particularly with New France and Seigneurial Systems or land use changes.
Using the virtual manipulatives aids the students in consolidating their understanding of equivalent fractions and common denominators, then transfer that understanding to a different task, using a different medium which demonstrates their understanding in environments other than those directly related to the specific learning environment (Dixon). Using a variety of mediums (virtual manipulatives, Smartboard tools, pencil and paper) students can consolidate their knowledge using anchored instruction and specific technology to augment their knowledge and increase their conceptual understanding.
Anne
References:
Dixon, Juli K, 1997. Computer use and visualization in students’ construction of reflection and rotation concepts. School Science and Mathematics, Volume 97(7), University of Nevada, Las Vegas.
Kathy-Ann Daniel-Gittens , Kelvin Thompson and Philip Carter (2014). Anchored instruction. In K. Thompson and B. Chen (Eds.), Teaching Online Pedagogical Repository. Orlando, FL: University of Central Florida Center for Distributed Learning. Retrieved April 3, 2017 from https://topr.online.ucf.edu/index.php?title=Anchored_instruction&oldid=3577
HI Anne,
Great in-depth lesson. I really like the problem-solving portion with the land sales and information that the students would need to work with and manipulate. I was wondering if this is something you would assess, or if it is a growth lesson? If this is a growth lesson would you provide a similar scenario in order assess it?
Would you consider any of the Jasper Woodley activities as they too are based in anchored instruction and I believe some of the activities dealt with fractions?
Catherine
I have used one of the Jasper lessons already and the students were very engaged in it. I can only find two of them, and they do not address everything I would need to address. I would be very interested in creating similar videos that do address some of the concepts like fractions in a more authentic way. I have a variety of activities such as the land use task. There are a couple using flags, and another one that is just a square to determine the fractions of the areas. I generally use these as growth lessons and then set them something fairly open as an assessment piece, such as a create your own flag using at least 8 areas and four colours. This helps to see if they really understand the fractions in relation to the whole.
Hi Anne,
I agree with Catherine- the land sales problem is an excellent way to apply these concepts to a real-life problem. I wonder how this would transition towards having students working with fractions purely with numbers and in more abstract ways as they prepare for math in later grades?
I’ve done similar diagrams when explaining adding and subtracting fractions, and it works reasonable well with multiplying, but dividing fractions is more difficult it seems. I think the interactive component would reduce the tediousness of having to draw the rectangles each time.
Thanks for the thorough lesson plan!
Thanks for the great feedback. In grade 7 they really seem to struggle with the concept of a whole, and the whole being different for different things, therefore a half is not always the same size. We will be looking at moving to a number line and more abstract numbers once they seem to have a good grasp of the underlying concept.
My grade 10 math students struggle with the same concept. I like the use of the SMART technologies for the problem solving process because it offers students options like erasing, refreshing, and manipulating without needing to entirely start again with each mistake. For example, if they colour something incorrectly, they can simply correct the mistake cleanly without needing to start a new sheet. Thanks for sharing!
Yes indeed, my students love using the Smartboard, and our board has the software loaded onto many of the laptops so even if they are not using the big board at the front, they can still manipulate the images on the smaller screen. It is not as dramatic, but it does the trick.
Hi Anne,
Thank you for contributing a math lesson to our discussion and for the resource on virtual math with fraction blocks! I like how you began with a common student error from your practice that then informed a rationale and a specific goal for a lesson. For example, a mis- or partial conception could be framed as students think fractions are determined by the denominator and the bigger the denominator the bigger the fraction (for example, 1/8 is bigger than 1/4) or that students think that fractions are two independent numbers. Students have a great deal of difficulty with fractions and understanding why they need a common denominator in order to add them. As this seems to be an issue each year with grade 7 students.
The LfU principles to undergird the lesson were mentioned. How might one or all of the particular phases of the framework support or guide the TELE you have created?
Thanks for producing an intriguing problem for students (and us) to solve, Samia
It’s interesting, if I viewed it correctly, to show the correct model and ask students to deconstruct it.