Reading about the LFU framework reminded me of the need for inquiry to be a bigger focus of Mathematical pedagogy. Below is a rough plan for how I would teach mathematical concepts using LFU:
Motivate
This stage of the model is designed to capture the attention of the audience and to realize the need to acquire new knowledge. I would “motivate” students by giving them an inquiry type activity that forces them to question what they currently know and what they need in order to solve the problem at hand. For example, one method of leading students into the Pythagorean theorem would be to ask students to measure the side lengths, and the hypotenuse of different right triangles in attempts to decipher a relationship between the side lengths and the hypotenuse. After students see the pattern, they can then use the pattern to make predictions on the lengths of the hypotenuse on right triangles despite not being given a picture of the triangle. Surely at that point, students would begin to question the pattern that they have observed. At that point, students are ready to be introduced to the Pythagorean Theorem, which puts their observations against established mathematical fact, that if a and b are side lengths of a right triangle, and c is the hypotenuse, that a^2+b^2=c^2.
Construct
After students have learned the key concepts, I will now provide activities that give them “direct experience” with the said concepts. This could be practical examples that involve the particular mathematical rule, or it could extend the activity introduced at the beginning of class. To continue the Pythagorean theorem example, at this point in time, I would expose students to problems that require the use of the rule, one practical example could be the following:
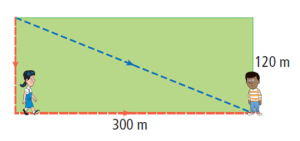How much farther would Jane walk to reach Albert if she went around the field, as opposed to directly across?
When I go over the solution to the problem, students would be receiving communication from myself, (or from other students in the class who have also solved the problem), which would allow them to build knowledge about the theorem and its uses.
Refine
After teaching the main concepts, I would provide other examples that offer a twist to the original problem to help students round out their understanding. Continuing the Pythagorean Theorem example, a classic refinement problem would be to ask the students to find one of the side lengths of the triangle given the length of the other side length, and the length of the hypotenuse. Solving this problem not only requires the students to understand the theorem, but forces them to literally reorganize the theorem so that they can work backwards to find the missing side length. It also offers students a chance to reflect upon their knowledge to see if they truly understand the theorem and its implications.
Hi Gary,
Thanks for your posting. This is a clear and structured plan for teaching Mathematics using LfU. I was wondering, in terms of communication and collaboration, would your students be working independently, and sharing ideas and strategies from this, or would they be working in partners/groups throughout the process as they attempt solutions? Depending on your approach, this would then lead into some different opportunities for reflection and further discussion.
Students should be allowed to communicate with others during this process, however, I really do think there is a greater benefit to working alone for the discovery phase. Students can, and should check their answers with other people as they work.