Author Archives: Gary Ma

Teaching the meaning of negative exponents

One of the common misconceptions by students when they first encounter the concept of a 0 exponent is to think that a number to the power of 0 is equal to 0. For example, many students believe that 2⁰ = 0. The correct result is actually 1, in other words 2⁰ = 1.

This misconception stems from their initial understanding of what exponents are. Students are taught that 2³ = 2 x 2 x 2, and so when they encounter the situation of 2⁰, it is natural to believe that it is equivalent to the number 2 multiplied by itself 0 times, which should give a result of 0. What students often fail to understand is that each time an exponent increases by 1, the value doubles. Taken in reverse, the value of 2⁰ should be half of the value of 2¹, which would give the correct conclusion that 2⁰ = 1.

To teach the concept of the 0 exponent, I have decided to take the TGEM approach as discussed by Khan (2010) , using an activity I created using the Desmos platform. The activity can be viewed here:

https://teacher.desmos.com/activitybuilder/custom/597642998fb671717b38af33

This activity encourages students to brainstorm, and share their thoughts as to what 2⁰ is equal to, before diving into an exploration that will eventually lead students to the value of 1 using a visual approach. The activity builds on the idea to discuss the concept of negative exponents and their meaning. I would utilize the above activity using the following steps:

Point students to the above link to allow them access to the activity. Ensure that a class code is created so that the class can join. Turn on teacher pacing for this activity to ensure students don’t work ahead, and to encourage discussion along the way.
On the first screen, pause and allow the students to read. Allow students to brainstorm what their initial thoughts are about the meaning behind the concept of a 0 exponent. Using the teacher dashboard, display the students input to look for commonalities in thinking.
On the second screen, ensure students understand that the numbers are doubling at each step. Students should be informed that they need to be precise, and that the “numbers are increasing” is will not adequately describe the pattern they see.
On the third screen, ensure students understand that the numbers are halving at each step. Students should be informed that they need to be precise, and that the “numbers are decreasing” will not adequately describe the pattern they see.
On the forth screen, ensure students can now reach the conclusion as to what the value of 2^0 is. Spend some time explaining the idea that a power with an exponent of 0 is equal to 1, no matter what the base is.
On the fifth screen, ensure students continue the pattern to reach a conclusion as to the meaning of a negative exponent.

Khan, S. (2010). New pedagogies for teaching with computer simulations. Journal of Science Education and Technology, 20(3), 215-232. Available in Course Readings.

How knowledge relevant to Math is constructed

How is knowledge relevant to math or science constructed? How is it possibly generated in these networked communities? Provide examples to illustrate your points.

Lampert (1990) provided an illuminating account of how she conducted her lesson on exponents to a grade 5 class in order to change the meaning of knowing, and learning Mathematics in her classroom to adhere much more closely to how Mathematicians would argue, and establish Mathematical facts. I believe that her method more closely resembles how knowledge in math is constructed.

Lampert argues that there is a sharp contrast between Mathematical practice and how the subject is perceived in popular culture and in the classroom. In the scientific community, Mathematical ideas are often questioned, with the assumptions frequently evaluated and foundations tested, and as such the subject is open to discussion and the possibility of uncertainty. This is in contrast to how mathematics is discussed in the classroom, as the teacher, and the textbook is believed to hold all the facts and are rarely questioned. It was also believed that the concept of “proof” and the challenging of assumptions are rarely brought into classroom practice.

Below are some of the practices that Lampert used in her class:

In starting a new unit, Lampert gave students wide open problems that encouraged participation, and discussion. For example, students were asked to find a way to determine the last digit in the expressions 6^4 and 7^4 without multiplying. Problems like these could be solve through a variety of strategies, and was open to student hypothesis and discussion. Lampert was not only looking for the strategy to solve the problem, but also the actual solution. This trains students in the act of forming hypotheses, and discussing their ideas. I also believe that this closely resembles how Mathematical knowledge is created: Mathematicians observe a problem in the real world, and conjectures are made about how to determine the solution to the problem.
Lampert wrote down student solutions on the board, along with their names. When students asserted that certain answers needed to be removed from the board because they were incorrect, the students were asked to provide reasoning as to why the answer is incorrect, and why the person who gave the answer thought the way they did. I thought this practice resembled academic discourse, as Mathematical proofs are often placed in the public eye, argued, and agreed upon before acceptance as fact.
Lampert followed, and engaged in the mathematical argument with the students in order to show students what it means to know Mathematics. Lampert made explicit the knowledge that she carried with her, and how she used that knowledge to carry an argument about the legitimacy of their proofs. The analogy Lampert used was one of navigating “cross country mathematics”. The teacher uses their knowledge to move along the path traveled by students on the mathematical terrain, and to help students move along. Instead of directing students along a carefully laid out path, Lampert suggests that teachers should show what it means to have mathematical expertise, and that it is more than being able to navigate down a straight and clean path, but rather the ability to navigate through sometimes rugged terrain.

Networked communities help generate mathematical knowledge by allowing information to be collected from a large population at once. One feature of the GLOBE library for example, is for students to contribute data to scientific studies (Penuel, 2004). Numerical data can be collected from a variety of sources, and analysed for patterns and possible relationships. I believe networked communities are a big frontier in mathematics. Many self driving car trials and experiments for example, is a result of data collected by a a large fleet of semi-autonomous vehicles.

Lampert, M. (1990). When the problem is not the question and the solution is not the answer: Mathematical knowing and teaching. American educational research journal, 27(1), 29-63.

Penuel, W. R., & Means, B. (2004). Implementation variation and fidelity in an inquiry science program: Analysis of GLOBE data reporting patterns. Journal of Research in Science Teaching, 41(3), 294-315.

Embodied learning, and the teaching of quadratic functions and equations

Through this week’s reading, I was able to conjure a new way to teach quadratic functions, and equations going forward that incorporates technology. In the following sequence of planned activities, I plan to incorporate a greater amount of collaboration between students, more opportunities to physically manipulate the information they are working with, and focus more on an inquiry based approach.

Learning about the graph of the quadratic function using graphing software

One of the major concepts students taking Pre-Calculus 11 need to learn is the quadratic function, and how the equation of the function determines various attributes of the graph such as its direction of opening, the location of the vertex, and its width. In teaching these different concepts, I plan to utilize Desmos Calculator to have students play around with different forms of the quadratic formula using the calculator’s slider function: http://support.desmos.com/hc/en-us/articles/202528919-Sliders

This Desmos activity I plan to create will leverage the “interdependence” of embodiment, embededness, and adaptation” (Winn, 2002) as students will physically manipulate the artificial environment I have created to learn, and adapt their knowledge about parabolas. An activity of this sort would also promote collaboration between students on a “mixed reality” type software where students have the opportunity for “physical interplay” of the graphs, which, according to Lingren (2013).

As for the choice of using Desmos Calculator over a standard graphing calculator, I am making the choice partly due to my own experiences with Desmos, but also to avoid many of the misconceptions related to quadratic functions pointed out by Powell (2015), many of which involves incorrect equation entry, and may be due to the standard graphing calculator’s small screen.

Relating quadratic equations and the graph of the quadratic function

Students frequently have difficulties connecting the concept of solving quadratic equations and working with the graphs due to their failure of seeing the relationship between the two concepts. To solve this problem, I would utilize another activity using the Desmos calculator. This time, I wish to use the calculator to showcase the relationship between the solution to the equation of the form 0=(x-a)(x-b), and the graph of an equation in factored form: y=(x-a)(x-b), vertex form: y=a(x-p)^2+q, and standard form: y=ax^2+bx+c. I would again utilize an activity involving sliders. I believe an activity utilizing sliders again in this instance, would allow me to reap the same benefits as the previous activity.

My questions for colleagues:

1. What are your experiences learning Mathematics with technology? How has graphing technology (whether it is on a graphing calculator or not) helped you with learning?

2. What do you see to the biggest problem in Mathematics education today?

3. What misconceptions in Mathematics have you struggled with in the past? How did you manage to get past them?

Lindgren, R., & Johnson-Glenberg, M. (2013). Emboldened by embodiment: Six precepts for research on embodied learning and mixed reality. Educational Researcher, 42(8), 445-452.http://www.move2learn.education.ed.ac.uk/wp-content/uploads/2015/04/Lindgren-2013-Embodied-Learning-and-Mixed-Reality.pdf
Powell, J. (2015). Solve the Following Equation: The Role of the Graphing Calculator in the Three Worlds of Mathematics. Interpreting Tall’s Three Worlds of Mathematics, 52(2), 11. Read one of the chapters from: https://scholar.google.ca/scholar?as_ylo=2013&q=embodied+learning+and+graphing+calculators&hl=en&as_sdt=0,5
Winn, W. (2003). Learning in artificial environments: Embodiment, embeddedness, and dynamic adaptation. Technology, Instruction, Cognition and Learning, 1(1), 87-114. Full-text document retrieved on January 17, 2013, from: http://www.hitl.washington.edu/people/tfurness/courses/inde543/READINGS-03/WINN/winnpaper2.pdf

TELE compare and contrast

After reading through the 4 different TELEs, a reoccurring theme is the flavor of constructivism that was apparent throughout. The principle of constructivism suggests that learners build knowledge through the continual modification of knowledge structure, modification that can be made after observing new information presented. For example, the WISE activities asks students to develop their own questions (visit their current knowledge on the topic), and afterwards presents to them new information that would allow students to better develop a cohesive account of different scientific phenomenon. The generate, evaluate, and modify (GEM) cycles can easily be seen as a remix of this concept. LFU presents a different take on knowledge acquisition in that it also focuses on how the knowledge is to be utilized as well, and it places an importance on how the knowledge is constructed, and applied.

The differences between the different TELE lies in the technology that is utilized and the different affordances offered by each. The examples of anchored instruction seen from the Jasper research involved the use of videos, which is a more antiquated use of technology, but allows for students to generate their own problems and sub problems to solve. The WISE activities were presented as information modules that students can walk through, and were more accessible to students at an earlier age. Other applications seen through the module such as MyworldGIS, and Chemland appealled to older high school audiences, but each allow different ways for students to access information and view the problem, or scientific phenomenon described in each activity or module. Overall, each study regarding the use of technology in the class suggested greater motivation, engagement, and student directed control over learning.

After module B, I am motivated to incorporate a higher number of technology based learning activities to help students teach math, but at the same time, I am now in greater awe of the amount of work that is needed to find, and/or to create the resources necessary to do so. I am more inclined to present students with basic information through direct instruction, and for them to build on top of the information through the use of technology to modify the knowledge that I have given to them. As for the challenge I know face, I am aware of a number of learning tools exist today for mathematics (Desmos learning activities, Geogebra, Geometer’s sketchpad, just to name a few), learning how to use these different tools to teach effectively (the TPCK needed) is quite a monumental task. This challenge calls for new modes of collaboration demanded of teachers, in that teachers may not only need to share teaching ideas and activities, but they may have to work together to build them if they never existed before.

Anchored Instruction
Theory	Learning goals
-Anchoring, or situating instruction in meaningful, problem solving context -Use of video technology allow students to freely access information in a problem posed to them	-Create an active learning environment -Students learn to generate their own problems, and sub-problems to solve -recalling and finding information in a story motivates students to engage in group work -connect to other parts of curriculum such as literature, history, and biology
SKI and Wise
Theory	Learning goals
-Web based learning activities create flexibly adaptive material to promote inquiry based learning. -Students build knowledge through developing their own questions (inquiry) and scaffolds their knowledge through new information presented to them in learning activities	-inquiry projects help students develop cohesive, coherent, and thoughtful account of scientific phenomenon -instruction pattern elicit student ideas, adds normative ideas, and supports process of combining, sorting, organizing, creating, and reflecting to improve understanding
LFU
Theory	Learning goals
-Knowledge construction is a goal directed process that is guided by a combination of conscious and unconscious understanding goals -The circumstances in which knowledge is constructed and subsequently used determine its accessibility for future use -Knowledge must be constructed in a form that supports use before it can be applied	-Overcome the “inert knowledge” problem (information that cannot be called upon when it is useful) -Motivate students to acquire new knowledge and to be curious -Incremental knowledge construction through observations of phenomenon or communication with others -Knowledge refinement and reinforcement through knowledge application
TGEM
Theory	Learning goals
-Generate, evaluate, modify with the use of computer simulations help students test their theories and modify existing knowledge	-Use technology to allow students to generate initial relationship between experimental variables. -Allow students to test assumptions. -Allow students to manipulate variables and to observe its effect

Transformations of functions – Using a Desmos Calculator activity

Being able to recognize how changes in the equations of a function could affect the shape of the function’s graph is a important component of BC’s Pre-Calculus 12 curriculum. The concept applies to all the different types of functions encountered in the course, and plays a role in helping students understand the shapes of different graphs.

This concept is challenging for students because it is easy to build misconceptions about the effect of changing certain variables in the equation. For example, adding a value of +k to a function f(x), would give an equation in the form of y=f(x)+k, and would translate the original graph k units up on the grid. On the other hand, replacing x with x+k, would give an equation of the form y=f(x+k), and would move the graph to the left, which is counter-intuitive because left is usually associated with negative numbers. This chapter has other similar concepts that could make it hard for students.

I have created a visual for a TGEM activity that could help students master the concepts in function transformation: https://magic.piktochart.com/output/23407439-etec-533-tgem-desmos

1. Generate: The teacher will preview two different graphs of parabolas and ask students to note the differences between the shapes of the graphs, or where they are located on the coordinate plane. Afterwards, students will be given the equations that correspond to each graph and be asked to make predictions on how different numbers in the equation could affect the shape and position of the graph.

2. Evaluate: The teacher will provide the Desmos activity “What is My Transformation”. The activity serves as an evaluative exercise for students and will allow them to determine whether the predictions they have set in the beginning of the lesson were correct.

3. Modify: After working through the activity, the teacher will regather the class, and ask for students to provide some of the facts that they were able to establish about modifying the equation of a graph. The teacher will also ask students to name some of the misconceptions that they came up with, and be asked to explain what led them to these incorrect assumptions. The point of emphasis is to crowdsource a list of possible areas where students could make mistakes.

LFU activities in Mathematics

Reading about the LFU framework reminded me of the need for inquiry to be a bigger focus of Mathematical pedagogy. Below is a rough plan for how I would teach mathematical concepts using LFU:

Motivate

This stage of the model is designed to capture the attention of the audience and to realize the need to acquire new knowledge. I would “motivate” students by giving them an inquiry type activity that forces them to question what they currently know and what they need in order to solve the problem at hand. For example, one method of leading students into the Pythagorean theorem would be to ask students to measure the side lengths, and the hypotenuse of different right triangles in attempts to decipher a relationship between the side lengths and the hypotenuse. After students see the pattern, they can then use the pattern to make predictions on the lengths of the hypotenuse on right triangles despite not being given a picture of the triangle. Surely at that point, students would begin to question the pattern that they have observed. At that point, students are ready to be introduced to the Pythagorean Theorem, which puts their observations against established mathematical fact, that if a and b are side lengths of a right triangle, and c is the hypotenuse, that a^2+b^2=c^2.

Construct

After students have learned the key concepts, I will now provide activities that give them “direct experience” with the said concepts. This could be practical examples that involve the particular mathematical rule, or it could extend the activity introduced at the beginning of class. To continue the Pythagorean theorem example, at this point in time, I would expose students to problems that require the use of the rule, one practical example could be the following:

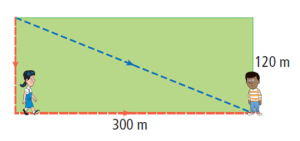How much farther would Jane walk to reach Albert if she went around the field, as opposed to directly across?

When I go over the solution to the problem, students would be receiving communication from myself, (or from other students in the class who have also solved the problem), which would allow them to build knowledge about the theorem and its uses.

Refine

After teaching the main concepts, I would provide other examples that offer a twist to the original problem to help students round out their understanding. Continuing the Pythagorean Theorem example, a classic refinement problem would be to ask the students to find one of the side lengths of the triangle given the length of the other side length, and the length of the hypotenuse. Solving this problem not only requires the students to understand the theorem, but forces them to literally reorganize the theorem so that they can work backwards to find the missing side length. It also offers students a chance to reflect upon their knowledge to see if they truly understand the theorem and its implications.

Rita’s swim – A WISE activity for high school math students

While attempting to edit the Amusement Park Challenge, I managed to find an activity inside that was hidden. It was an activity called Rita’s Swim. One modification I’d add to the Amusement Park Challenge is to activate Rita’s Swim, and make it part 2 of the Amusement Park Challenge activity.

The modified Amusement Park Challenge can be found here: http://wise.berkeley.edu/previewproject.html?projectId=20977

To summarize the activity, part 1, or the Amusement Park Challenge, requires the student to inquire about the tenets of safe/thrilling amusement park ride. The student will then have to construct distance vs. time graphs for either a safe/thrilling amusement park ride. The activity concludes with each student sharing their ride with other students. Rita’s swim activity is a similar investigation into the relationship between distance vs. time graph, and the actual physical movement of an object, however, this time, the graph accompanies a story describing Rita’s swim across a pool.

Although this activity is designed for elementary school students, it can be modified to give high school students a basic inquiry activity about slope and rates of change. The activity as currently constructed, would be an excellent inquiry activity to begin a lesson on rates of change – I would give students an opportunity to work through the lab, which should provide students an opportunity to apply what they know about the real world (their current understanding of speed, and rates of change) to graphs. As students progresses through the WISE activity through its two parts, students will gain an opportunity to reorganize their knowledge, and make corrections, as the bumper car and its movements would be visible to students after they have modified their graph. After working through the Amusement Park Challenge and Rita’s swim, students should have a fair well built understanding of the connection between speed, direction, and the graphs that represents change in each of these properties. After the activity, I would then begin getting into the mathematical portion of the lesson. I would use the graphs to introduce the concept of a rate of a change, which in this case would be the slope of the curve that is formed. I would then introduce the formula for slope: m=y2-y1/x2-x1, and use the formula calculate the slope for different lines to show that the slope is representative of speed.

I believe my lesson takes a constructivist approach and have followed the principles of SKI closely (Linn, 2004). 1) The students thinking about speed was made visible to them via the Amusement park/Rita’s Swim activity 2) The science behind speed and graphs was made accessible to students due to the guided nature of the WISE activity, 3) and social support was given to students as they were given an opportunity to share their thrill ride after the conclusion of part 1. Feedback would be provided by the WISE activity throughout, and during student discussions of the various created thrill rides.

Williams, M. Linn, M.C. Ammon, P. & Gearhart, M. (2004). Learning to teach inquiry science in a technology-based environment: A case study. Journal of Science Education and Technology, 13(2), 189-206. Available in Course Readings.

Anchored Instruction in the modern mathematics classroom

As a high school math teacher, I was excited to read about the Jasper series and think about how it could have been implemented today. Although the concept of TPCK did not exist back in the 1980s when the series was first introduced, it was clear that teachers that wished to teach using the series had to have had experience working, and teaching with technology (needed to know how to use a video, and teach students how to learn from it). If the same series was used today, I can imagine that students would have been able to view, or construct the problem in a multitude of ways:

1.Video, or VR simulations – When Rescue at Boone’s Meadow was first introduced, the problem was given through video, with the Cognition and Technology Group at Vanderbilt (1992) suggesting that the video based format increases motivation, and allows the videos to be searched much more easily. One can imagine that such a scenario be delivered using modern day simulation technology like VR that could allow students to live through the problems. One can also imagine being able to simulate their solution through virtual reality. Although this technology is still undeveloped, we are pretty close to seeing VR entering the educational realm in full force.

The concept of teaching with video is widespread in today’s education system, especially for mathematics. Many YouTube channels, such as the Khan Academy, offer a variety of mathematical tutorials, and lessons that students utilize in order to learn concepts independently from school. As a teacher though, I believe that if one were to utilize videos effectively, one would often have to rely on videos produced by other teachers, as the time and resources required to create a video of high quality is often too much for a single teacher. As a result of that, the instructor must always adapt their teaching style or methods around what is seen in the video. This is not a tremendous issue, but when teachers use videos, they are often placed in more of a facilitator role, as opposed to being more direct with their teaching. Although this is encouraged in many modern research, indirect teaching may be resisted by certain students.

2. Online discussion of solutions – Rescue at Boone’s Meadow was introduced before the internet era, and as a result, discussions around solutions would take place synchronously in a classroom across a couple of periods. However, in today’s internet age, one could imagine online resources in playing a large role in influencing students development of a solution. Just like a video game, students across the country could pick apart, and dissect the situation faced by Jasper in the scenario, and naturally, multiple feasible rescue methods are likely to be found on the internet. If students were resourceful and found these solutions online and used them to develop their own solutions, how should teachers assess for student learning?

In terms of modern mathematical tools such as CTC math, IXL, etc. I believe that many of these tools seem to oppose anchored instruction, and the more popular these tools get, the farther we deviate from the design principles discussed by the Cognition and Technology group at Vanderbilt. Tools like IXL have their place on mathematics education in that they offer students an excellent resource to practice skills that can learn through repetition (for example, arithmetic, algebra, equation solving), but they often offer very one dimensional ways of delivering information. Anchored instruction relies on linkage across curriculum and student independence in formulating their own problems and solving them, whereas online tools such as IXL do the opposite, they create all the problems for the students to solve.

It would appear part of having a strong base of TPCK is knowing when to utilize technology, and understanding what the benefits are consequences are when we adopt a new software for the classroom. We can introduce students to IXL and Mathletics and encourage students to work on problems, but sometimes it takes time away from giving students situations like Rescue at Boone’s Meadow, where a large emphasis is on discussion and generative problem solving. An expert will need to properly balance both teaching activities in the classroom.

Barron, L., Bransford, J., Goin, L., Goldman, E., Goldman, S., Hasselbring, T., … & Vye, N. (1993). The Jasper experiment: using video to furnish real-world problem-solving contexts. Arithmetic Teacher, 40(8), 474-479.

Cognition and Technology Group at Vanderbilt. (1992). The Jasper experiment: An exploration of issues in learning and instructional design. Educational Technology Research and Development, 40, 65-80.

PCK and TPCK as a math teacher

I first came across the concept of PCK and TPCK in ETEC 511 last summer and the concept has stuck with me since then because I think it perfectly captures what I wish to learn from my experiences in the MET program. Before I was a Math teacher, I worked several co-op jobs in the IT industry, where I worked with many people that had strong technical backgrounds. They had experience not only in using technology, but also in building software and the likes. Upon reflection, if those people were put in a classroom, would it make them effective teachers? Not necessarily, because teaching with technology versus utilizing technology are very different things. On the flip side, being a seasoned veteran teacher doesn’t mean that they would be able to pick up any piece of educational software, and be effective at using it to teacher. Between knowing how to use technology, and teaching, there must be a bridge between these two very different knowledge domains, and I think Mishra and Koehler (2006)’s TPCK presents the idea quite well.

One of the most classic example what I consider to be TPCK in the realm of Mathematical teaching comes with the use of graphing technology. As a high school math teacher, one of the most important tools at the senior levels is graphing technology because it allows learners to visualize many of the concepts taught in class. The graphing calculator is a tool that can be used to simplify calculations, to assess learning, and for users to potentially explore creating mathematical tools through programming. In order to effectively teach with a graphing calculator, a teacher must first have the requisite mathematical knowledge and also the pedagogical skills to deliver the content, or otherwise, they must have the PCK needed to teach the course. TPCK takes this knowledge to another level, as teachers must learn ways to teach students how to use the calculator effectively, or in different situations, use graphing software to demonstrate concepts to students.

Mishra, P., & Koehler, M. (2006). Technological pedagogical content knowledge: A framework for teacher knowledge. The Teachers College Record, 108(6), 1017-1054. Text accessible from Google Scholar.

My vision for the technology enhanced classroom – 3 important facets.

The term “Mindtools” and how they are used in a classroom setting described by Jonassen (2011) best mirrors my ideal vision of how technology can be used to enhance a learning experience in the classroom.

I believe that technology should enhance the learning experience in 3 ways. First, technology should be used to engage and capture the learner’s attention. Use video display technology to show videos to take students out of the classroom and spark interest in a new topic, or use technology to help perform demonstrations that capture the audience’s attention. Secondly, technology use can help students make meaning of the world around them. Technology can be used to give students different visual perspectives of scientific or mathematical concepts. The use of simulations and graphing devices can give students hands on experience and allow teachers a better way to engage in constructivist practices. Finally, technology in the hands of the teacher can allow for different modes of assessment, as adaptive learning technology improves, teachers can utilize technology to better determine student deficiencies and misconceptions and help the teacher plan strategies, or better allot lesson time to address student concerns and problems.

Jonassen, D. H. (2000). Computers as mindtools for schools, 2nd Ed. Upper Saddle River, NJ: Merrill/ Prentice Hall. Retrieved from Google Scholar: http://scholar.google.com/scholar?q=Jonassen+mindtools&ie=UTF-8&oe=UTF-8&hl=en&btnG=Search