Author Archives: wincherella

My TELE – Vision

As my final project I have created a TELE for middle school teachers to use as part of the Heat Energy Unit required in the Ontario curriculum. It is a website that is scaffolded so students can work through it at their own pace with each lesson building upon the last. Embedded are simulations and physical labs for students to have both hands on and online experiences to help consolidate their learning of the concepts.

The rationale and introduction to the TELE is a website that can be found here:http://winchetec533-tele.weebly.com/

And the student website with the lessons can be found here: http://winchscience7-heat.weebly.com/

Part of my motivation for creating this TELE is to use it with my students in my class this year. I am excited to see how they react to the simulations and the WISE projects as part of their learning.

If you choose to check it out, I would love to have your feedback.

Anne

Geography TELE

A few years ago I was searching for a new way to deliver the grade 7 geography curriculum. We had just received a class set of chrome books for the school and I thought I would combine geography and technology by creating a website the students could work through at their own pace. I included some mini lessons and specific tasks for them to complete. It was sort of a first attempt at the TELE if you will. I thought I would share it with you here. Feel free to check it out, use it or adapt it.

http://winchgeography7.weebly.com/

Anne

Virtual Fraction Fun

Mathematics

Targeted Group: Grade 7

Format: Number Sense and Numeration – Adding Fractions

Misconception: Adding fractions without finding common denominators or equivalent fractions.

Rationale:

Students have a great deal of difficulty with fractions and understanding why they need a common denominator in order to add them. As this seems to be an issue each year with grade 7 students I thought it would be a good idea to find new ways to address the concept.

Goals:

Students will be able to add fractions competently with like and unlike denominators, finding equivalent fractions in authentic problems.

Materials: Virtual fraction manipulatives

http://www.mhhe.com/math/ltbmath/bennett_nelson8e/VMK.html?initManip=fractionBars

Smartboard notebook software – Specific lesson plans
Authentic addition of fractions questions.

Process: This can be done individually or in pairs.

Step 1:

Give students a step by step adding fractions task sheet with three different tasks. The step by step process allows the students to see how the common denominator is found and how to add the fractions.

Step 2:

Direct students to the virtual manipulatives at the above URL. This would be in their Edmodo folder already so they just have to click on the link.

Step 3:

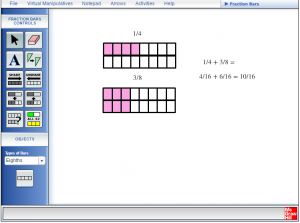
Direct students to create the model shown on the task sheet on the virtual page using fraction blocks. Students should write the addition statements on the virtual page, and then transfer them to their task sheet. They should continue to do this for all the questions on the task sheet.

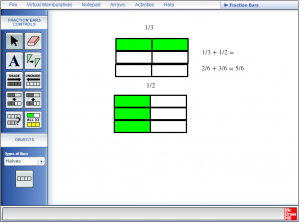
Step 5:

Ask the students to create their own addition problem using the fraction bars for the other students in the class to try. Students should be sure to draw this on their task sheet including the correct addition statements.

Consolidation Activity: Smartboard Notebook Lesson

Task:

Introduce students to the Land Ownership task. Show them the picture of the land split into various areas for different owners in SmartNotebook. Students can use this software on the laptop computers using the mouse.

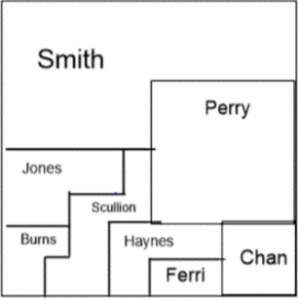
Work with a partner.

The map shows land owned by 8 families.
Determine what fraction of the land each family owns.
Four families sold land to the other four families.
Use the first map clues to help you draw the new map. You can use the back of the sheet to do this.
Write the addition to show each of the transactions.

CLUES

When all the sales were finished, four families owned all the land – Smith, Perry, Haynes, and Chan.
Each owner can walk on their land without having to cross another person’s property.
Smith now owns 1/2 the land.
Perry kept 1/2 of her land and sold the other half to Chan.
Haynes bought land from two other people. He now owns 3/16 of the land.
Chan now owns the same amount of land as Haynes.

Students use the tools in SmartNotebook to colour in the areas owned by each family and manipulate the shapes to find the smallest piece in order to determine the common denominator. Once they have done this, students find the equivalent fractions for each of the owners property showing the fraction in equivalent form and simplest form. For example: Perry = 1/4 or 16/64.

When they have found all the equivalent fractions it should be easier for them to rearrange the fractions for the four families to own all the land according to the clues. They need to show the new configuration on their screen or paper, and show the addition statements that go with their solutions.

Education Theories:

The educational theories that are associated with this lesson plan are Learning for Use and Anchored Instruction.

Learning for Use framework is a pedagogical framework that integrates the content with the processes of the subject matter. Using the virtual manipulatives allows the students to visualize the process of creating the equivalent fractions, how a common denominator is determined, and then how the two fractions are added together. Since the content is being able to add fractions with unlike denominators, the manipulatives allow the students to try a lot of different combinations of fractions to find their equivalents and add them. The virtual manipulatives also allow the students to discover these concepts for themselves, and build upon that understanding using the tiles to create a number of different combinations.

Anchored instruction is the process of presenting instruction in the context of an authentic environment with problems or issues which learners must resolve. The problems or issues which are presented to learners in the authentic environment are “anchors” which link learning of content and skills to authentic tasks and activities in which the learning must be used (Gittens, Thompson, & Carter). Although this is not a true representation of anchored instruction, the concept of buying and selling parcels of land is a real world connection. It is difficult to find authentic problems using fractions that the students would recognize. This problem could be related to their history or geography lessons particularly with New France and Seigneurial Systems or land use changes.

Using the virtual manipulatives aids the students in consolidating their understanding of equivalent fractions and common denominators, then transfer that understanding to a different task, using a different medium which demonstrates their understanding in environments other than those directly related to the specific learning environment (Dixon). Using a variety of mediums (virtual manipulatives, Smartboard tools, pencil and paper) students can consolidate their knowledge using anchored instruction and specific technology to augment their knowledge and increase their conceptual understanding.

Anne

References:

Dixon, Juli K, 1997. Computer use and visualization in students’ construction of reflection and rotation concepts. School Science and Mathematics, Volume 97(7), University of Nevada, Las Vegas.

Kathy-Ann Daniel-Gittens , Kelvin Thompson and Philip Carter (2014). Anchored instruction. In K. Thompson and B. Chen (Eds.), Teaching Online Pedagogical Repository. Orlando, FL: University of Central Florida Center for Distributed Learning. Retrieved April 3, 2017 from https://topr.online.ucf.edu/index.php?title=Anchored_instruction&oldid=3577

Knowledge Construction in STEM

Student engagement is an ongoing concern for most educators as disengaged students are passive, not actively engaged in constructing new knowledge. Students become engaged when the activity, not only captures their imagination, but also has relevance for them. Inquiry is one way of igniting the spark of interest in students which is essential to science learning. Educationally effective programs are those in which products are not emphasized, inquiry is sparked, open-ended questions are generated, and students actively participate and appear involved (Gutwill and Allen). The ultimate engagement is to put the learner in charge of learning, and inquiry learning does just that.

However, the learning needs to be anchored to something that is relevant to the learner in order for new knowledge to be constructed and retained for future retrieval. GLOBE researchers have suggested that GLOBE is an example of anchored instruction, and although this appears to be the case in that it is conducted in a realistic setting to respond to a realistic inquiry, the students themselves are only collecting and submitting the data, not analyzing it, looking for trends, or making conclusions about the significance of the data they are collecting. Penuel and Means (2004) note that “students are not just collecting data as part of an isolated laboratory experience but as contributors to actual scientific studies” (p. 296). I agree that the students are an integral part of the data collection but I disagree that the students are doing “real science investigations” (295) as they are not involved in using the data to discover its significance and do not take part in the actual scientific studies. Scientists use the student collected data in their own investigations (Penuel and Means, 296).

A key assumption is that students can collect scientifically useful data, however it must be collected in accordance with specific protocols and be reported consistently over time. (Penuel and Means, 296). This can be somewhat onerous for the students and some of the participants find submitting the data repetitive. Because the students are not involved with using the data, the relevance of the collection becomes remote, and the students lose interest because it becomes a chore, rather than an exciting inquiry into science. Students in these schools are not getting the realistic picture of the nature of scientific investigation that the authentic data collection is intended to provide (Penuel and Means, 309).

The GLOBE program provides learning activities that can be implemented by the teacher at the same time as the students are doing the data collection. The GLOBE philosophy is one of providing resources but leaving the decisions concerning curriculum and pedagogy up to the teachers because the teacher’s choices are not threats to the program’s scientific and educational goals (Penuel and Means. 297). This means that the learning material is disconnected from the actual scientific inquiry. Students and teachers could use the learning materials and the subsequent data collection to pose their own questions, collect their own data, analyze it, and formulate explanations, but this would be outside of the inquiry being done by the GLOBE scientists. If this were the case, then the program would be anchored instruction, but as it stands now, it is just a small part of a larger scientific inquiry being completed outside of the program.

References

Butler, D.M., & MacGregor, I.D. (2003). GLOBE: Science and education. Journal of Geoscience Education, 51(1), 9-20.

Kountoupes, Dina L., Oberhauser, Karen S., Citizen science and youth audiences: Educational outcomes of the monarch larva monitoring project. Journal of Community Engagement and Scholarship, Vol 1, 1

Penuel, W.R., & Means, B. (2004). Implementation variation and fidelity in an inquiry science program: Analysis of GLOBE data reporting patterns. Journal of Research in Science Teaching, 41(3), 294-315.

Learning in Artificial Environments

Like a few of my classmates, I have found myself intrigued with many of the readings this week, moving from one article to another as I become more involved in the different aspects of this type of learning, with each new article giving me something new to ponder on. The idea that most caught my interest was that of immersive participatory augmented reality simulations as posited by Dunleavy, Dede, & Mitchell, and the link to gaming environments. I have long been fascinated by the idea of using game elements in the classroom to increase student engagement and motivation, and AR simulations provide the means to implement this. The technology-mediated narrative and the interactive, situated, collaborative problem solving affordances of the AR simulation were highly engaging, especially among students who had previously presented behavioural and academic challenges in the classroom (Dunleavy, Dede, & Mitchell).

Winn notes that cognition is embodied in physical activity, that is embedded in the learning environment, and that learning is the result of the adaptation of the learner to the environment and the environment to the learner (Winn, 2002). This idea is corroborated by further research suggesting that learning and cognition are complex social phenomena distributed across mind, activity, space, and time. A student’s engagement and identity as a learner is shaped by his or her collaborative participation in communities and groups, as well as the practices and beliefs of these communities (Dunleavy, Dede, & Mitchell). The idea of collaboration using Participatory Simulations is reiterated by Collella in the Participations Simulations Project using the Thinking Tags. Participants personal connections to the educational situation enable them to bring their previous experiences to bear during the activity, establish strong connections to the activity and the other participants, and to be able to draw upon their experiences for the future (Collella, 2000).

The idea of using the area around my school to create an AR activity, such as the one presented in Alien Contact, fired my interest in creating such a project. This would be a great way to embody physical activity, science and math into an already familiar environment using digital resources to create the simulation. I was also intrigued by the idea that the narrative was an important component to the activity. This is a gaming feature to engage the students the background story is most important. The problem solving using science and math is embedded in the story. The most significant affordance of AR is its unique ability to create immersive hybrid learning environments that combine digital and physical objects, thereby facilitating the development of process skills such as critical thinking, problem solving, and communicating utilized through interdependent collaborative exercises, its ability to blend a fictional narrative with the real and familiar physical environment such as the school playground (Dunleavy, Dede, & Mitchell).

However, as all of the participatory simulations I discovered used specific technology, perhaps not available to all schools, my questions are these:

How can we use technology already in the hands of our students, such as smart phones or tablets, to engage them in AR participatory simulations?

How can we best leverage the hybrid environments of digital and physical artifacts to create a rich, collaborative inquiry integrating math and science?

How can we interest teachers in integrating AR type simulations into their classroom program?

Resources

Vanessa Colella (2000) Participatory simulations: Building collaborative understanding through immersive dynamic modeling, Journal of the Learning Sciences, 9:4, 471-500 doi:10.1207/S15327809JLS0904 4

Dunleavy, M., Dede, C., & Mitchell, R. (2008). Affordances and limitations of immersive participatory augmented reality simulations for teaching and learning. Journal of Science Education and Technology,18(1), 7-22. doi:10.1007/s10956-008-9119-1

Winn, W. (2003). Learning in artificial environments: Embodiment, embeddedness, and dynamic adaptation. Technology, Instruction, Cognition and Learning, 1(1), 87-114. Full-text document retrieved on January 17, 2013, from: http://www.hitl.washington.edu/people/tfurness/courses/inde543/READINGS-03/WINN/winnpaper2.pdf

Technology Enhanced Learning Experience (TELE) Synthesis

In module B we explored four foundational technology-enhanced learning environments (TELE). These were Anchored or Situated Instruction featuring the Jasper Series, Web Inquiry Science Environment (WISE) and Scaffolded Knowledge Integration (SKI) using the science and math based WISE projects available on their website, Learning For Use (LFU) model with MyWorld GIS and ARCGIS mapping systems, and Technology – Generate, Evaluate, Modify (T-GEM) demonstrated with Chemland.

The advantage of TELEs is the affordance to provide creative technology integration that supports effective pedagogy in the science and mathematics classroom. Technology proficiency for students and the integration of technology into the classroom is critical for today’s 21^st century learners. However, in order to maximize positive results, the pedagogical approach of technology should be encouraging students to make the activity and the content personally meaningful (Barab, 2000), which these four foundational learning environments accomplish.

This synthesis compares and contrasts the four TELEs explored throughout this module in different ways. First I created a graphic web using Inspiration, in order to organize my ideas and understanding into categories. This allowed me to synthesize the roles and affordances of each TELE. The second comparison took the form of a Venn diagram allowing me to consolidate the similarities and differences between the four TELEs. These diagrams are included below (follow the link for readable copies).

Technology Enhanced Learning Experience pictures

The Jasper Series was based on providing a real life context for solving mathematical challenges for students. It allows for a much more student centred approach to using mathematics than traditional text book lessons. This series also addresses the age old question of “why do we have to learn this?” as the math is embedded in the stories and within the challenge. This method promotes a method of learning which is rooted in reality and anchors the concepts to problem, providing students with a real purpose to understanding the math rather than just learning it out of context and by rote. The video itself is not customizable, however I think the challenges could be changed or modified in different ways to suit the information provided in the video.
(I tried out the Rescue at Boone Meadow video with my class of grade 7 students and found they were engaged in the story (context) and were quick to figure out what mathematical information was required in order for them to try to solve the problem. None of them whined about it being too hard or too much for them).

WISE and SKI – was a specific platform providing a wide range of topics that made science accessible to students and made thinking visible through simulations and models. It allows for collaboration as well as a student paced model as they can work through the project at their own pace or one suggested by the teacher. Teachers can modify the projects to fit their own classroom expectations. Although there is a wide variety of projects available on WISE, they are all specific in nature and generally address a specific scientific concept.

LFU – MyWorld GIS – is a framework which allows for many constructivist principles, such as learning through constructing and modifying existing knowledge, learning is initiated by the learner therefore the learner is engaged in order to build upon pre-existing knowledge and understanding. This platform is easily modified by the student or the teacher just by choosing different data sets with which to manipulate the maps. In Learning for Use platforms, the use is quite specific in that the data here is specifically around maps, mapping, and geographical information. These premises could be integrated into other areas of curriculum, but still with a specific purpose.

T-GEM – Chemland is a specific platform aimed at secondary or post-secondary students. The ideas are sophisticated and although the students can manipulate the simulations to some degree, they are focused on one aspect of the concept. Teachers cannot modify the simulations to suit the conditions in their own classrooms. The T-GEM framework is easily adaptable to other types of simulations where students can manipulate the data, evaluate, and modify their understanding as more information is acquired.

Reflection

As a middle school teacher in an elementary school setting, I found some of these platforms intriguing and suitable for use with my students, and others I found way too difficult for them to manage without frustration, or the concepts were too advanced for the curriculum. However, all of them followed the tenets of constructivism and problem solving. These approaches such as anchored instruction, problem solving, scaffolding, knowledge construction, and evaluative reasoning, should not be limited to just mathematics and science, but could be applied to all areas of the curriculum. One of the greatest affordances of the TELE is the power of visualization and being able to add a visual image, model, or simulation to the students learning experience.

Two key concepts in my evaluation are student misconceptions and constructing new knowledge. Misconceptions are identified, created or dispelled by constructing new knowledge and modifying thinking to adjust for the new understanding. With guidance from the teacher, along with built in reflections in the technology, misconceptions can be corrected or modified. This is an important step in order to make sure that misconceptions are not perpetuated or new ones created. I now have a much greater awareness of how students create misconceptions, and how to find efficient, meaningful ways to dispel these misconceptions.

The incorporation of TELE is something all teachers can benefit from, particularly those in math and science disciplines. Pedagogy matters when it comes to any instructional tool and why the implementation of any TELE should be rooted in effective teaching strategies and not just something used without purpose. My pedagogical approach and purpose for using technology is the most important factor when it comes to choosing a platform to use with my students. Teachers must use technology with intention and purpose, the ability to modify some of the TELEs speaks to this, whereas others would need to be chosen carefully to make sure they fit the parameters and meet the needs of the lesson and the students. Although I strive to make this a priority in my own teaching, I realize that there is so much more out there than I can integrate to make my students learning environment much richer.

Anne

Jasper in Action

I really liked the premise of the Jasper series, in spite of the fact they were a little dated, and so I tried one of them out with my grade 7 class as part of their Kingdom Day Challenge. I searched them out and found a couple of the original videos on youtube, Boone Meadow and the Recycling Challenge. Today we watched Boone Meadow as it ties in with a few things we are doing in class. The students worked in their Kingdom Groups of 5 students in each group. The groups are heterogeneous.

The students were quite engaged in the video and it did not take too long before a few students realized that they should be making notes about the information being given in the video. One student asked if we could replay the first bit so they could make notes about the information and I obliged. Other students soon caught on and started to keep notes also. They seemed to enjoy the characters in the video and appreciated the story line. Once the challenge question was given, the students started to figure it out and soon realized they needed some of the other information they had seen in the video, but had not realized they might need later. The beauty of the video on the Smartboard is they could go back and view the actual frames to find the place in the film for the information they needed. They could move the pointer back and forth as many times as required in order to find the information, and many of the students took advantage of this. The picture below shows a couple of the students checking this out.

All in all, I found the exercise quite rewarding in that the students were engaged and motivated to find the solution to the challenge. There were a few different solutions and I am looking forward to the discussion we will have around them tomorrow.

Anne