Requirements of the body and conditions under which the body works is not constant. Therefore, the functioning of the urinary system cannot be constant!

  • You kidneys help maintain water balance in your body (part of homeostasis)
  • Two hormones are needed: ADH and Aldosterone!

First of all:

  • Diuretic – Anything that increases urine production

Natural Examples: Alcohol, sativa, caffeine, dandelion

  • Antidiuretic – Anything that reduces urine production

Natural Examples:Licorice, Potatoes

Antidiuretic Hormone (ADH)
  • Secreted by posterior pituitary gland in response to lower blood volume (remember the hypothalamus screens the blood and determines control of pituitary gland)
Figure 1: ADH – Posterior Pituitary
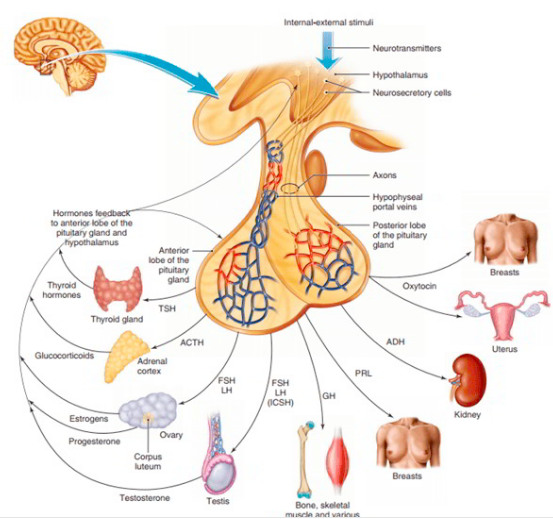
  • Hormone binds to receptor sites on collecting ducts.
  • Increases permeability to water -> more water reabsorbed into blood
  • Combats low blood volume, low blood pressure.
Figure 2: ADH release and target
Figure 3: ADH function
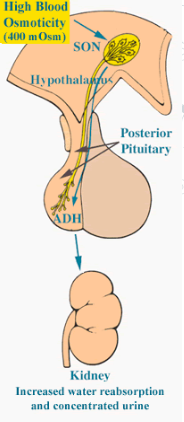
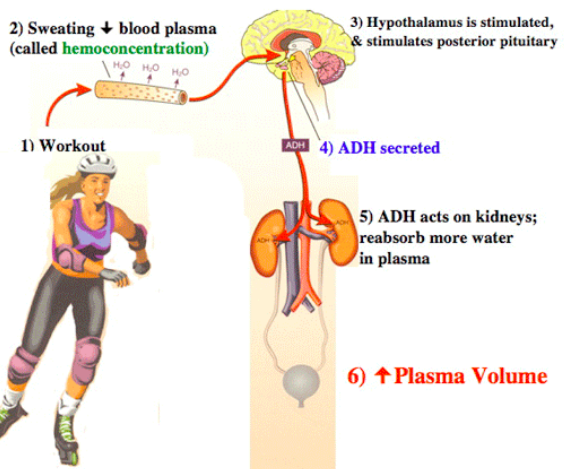
  • Dehydration causes ADH to work on this pathway, but also causes special cells in the hypothalamus to shrink which triggers a thirst response
  • Alcohol is a diuretic because it stops ADH production.
Figure 4: Chemistry of a hangover
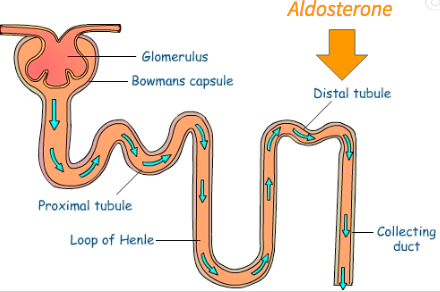
Aldosterone
  • Also helps return water to the blood.
  • Released from adrenal cortex (top of adrenal gland on kidney) when blood pressure drops
  • Receptors in blood vessels near start of nephron notice pressure drop.
  • This starts a chain reaction which ends with aldosterone release
  • Usually in response to low Na+ concentration.

Brief note:

Aldosterone is increased based on low Na+ – ADH decreases!

Likewise, ADH is increased with low blood volume, Aldosterone descreases!

  • Aldosterone increases the amount of Na+ reabsorbed at the distal convoluted tubule.
  • Therefore, Na+ retention in plasma increases.
  • Water will passively get reabsorbed as well, increasing blood pressure (through an increase in blood volume) and concentrating urine
Figure 5: Aldosterone targets distal tubule
Summary:
  • Dehydration = bad
  • Low blood volume is assessed by hypothalamus.
  • Posterior pituitary releases ADH
  • ADH – binds to collecting duct, more water reabsorbed into blood.
  • Low blood pressure – measured by receptors near nephron
  • Chain reaction causes release of aldosterone from adrenal gland
  • Increase Na+ reabsorption here
  • Water is reabsorbed due to this.