Hmmm… I’m not sure if this is a legitimate post for this week so I will likely address the second question later on. Anyway, it seems as though my post from the TGEM week fits nicely into our task requirements. I definitely put some hours into this lesson, so here goes… (the lesson is attached to the end of this post)
Having yet to finish reading the “related literature”, I think I will return with more thoughts to add to my PhET lesson! To be continued!!!!
<insert dramatic yet Monty Python-esque interlude music>
I’m back! The two papers that I read today were “Reality versus Simulation” and “Fifty Years of Thinking About Visualization and Visualizing in Mathematics Education: A Historical Overview”. ( Srinivasan et al, 2006; Clements, 2014). Relating these reading to my guided inquiry-based, simulation, T-GEM lesson…
- “Reality versus Simulation”
- the authors conceded that there were no distinguishable quantitative differences between students’ learning outcomes via a simulation or an actual lab
- the big takeaway was that the majority of students perceived that the simulation was not as valuable of an experience than actually setting up and testing with real equipment; the simulations seemed inauthentic to students; professors perceived no difference in modalities
- the authors suggest there may be benefits to having open-ended discussions with students to help them appreciate the validity and worthiness of using a problem-free, time efficient simulation
- adding this type of discussion to Mt. Gravitation would be relatively simple to do; I refer to the simulation throughout the unit already, however, a more directed discussion could help mitigate students’ negative perceptions
- “Fifty Years of Thinking About Visualization and Visualizing in Mathematics Education: A Historical Overview”
- very engaging paper for mathematics educators; very readable and contains engaging problems throughout; I subjected my mathematically gifted, 10 year old to the H-Shape problem– he nailed it and when asked about the method he used, he used analytical approaches over visual approaches (very interesting!!!)
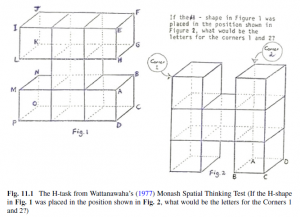
Wattanawaha’s Monash Spatial Thinking Test, (Clements, 2014)
- there are many interpretations of what mathematical visualization entails
- one research process is to categorize students using the Mathematical Processing Instrument where subjects answer problems and solutions are categorized as visual, verbal-logical or neither in nature.
- it turns out that students who utilize verbal-logical methodologies primarily, perform better on math tests
- the author pushes the reader to think of ways to exploit a visual learner’s strengths to make them more successful in the mathematical classroom setting
- relating these ideas back to my lesson reminds me that some of students will be able to interpret the graphical relationships connecting force to separation distance, more easily than others; my students have inherent strengths– to be able to work with those strengths yet also assist them develop their “non-strengths”, will continue to be a goal of mine as I guide them through their learning
- another interesting takeaway from this paper was that visual learners tend to apply visual strategies to problems that are optimally solved using verbal-logical strategies; also verbal-logical learners will tend to favour verbal-logical strategies when a visual approach is more efficient; as educators, we can introduce problem strategies that “go against the grain” of our students’ preferences, in order to maximize their overall experience and comprehension
- very engaging paper for mathematics educators; very readable and contains engaging problems throughout; I subjected my mathematically gifted, 10 year old to the H-Shape problem– he nailed it and when asked about the method he used, he used analytical approaches over visual approaches (very interesting!!!)
Thank you Catherine for your review of these two papers and for contributing to a discussion on math education and visualization. The Clements paper has a host of math problems to try out which will be interesting for all of us. Srinvisan et al (2006) tackle an issue with regards to simulation and whether it is “real” or “made up”. The use of glass box simulations can help to mitigate this issue and address the mechanics underlying the simulation and how it produces the information. In the class that was the subject of study for one of my papers (c.f. Khan, 2007), the teacher took some time to explain the scientific process of how one data point was established in the simulation.
This discussion involved the history and nature of science. And since we’re talking history, it’s interesting to note also that simulation in their own right have been the basis of a recent Nobel Prize (see the Nobel Prize in Chemistry 2013 which was awarded jointly to Martin Karplus, Michael Levitt and Arieh Warshel for the development of multiscale computer models that simulate complex chemical systems). In the 1970s, when these three scientists did their seminal work, there were either simulations for doing chemistry that performed classical mechanics or others that performed calculations at the quantum level. Classical programs gave chemists a good representation of how the atoms were positioned in the molecules but only displayed molecules in a state of rest. During reactions, molecules are filled with energy; they become excited. Simulations based on classical physics had no way of representing all of the various energy or quantum states of atoms. When scientists wanted to simulate let’s say the function of enzymes to better understand their role in important biochemical processes, they turned to quantum physics, the theory where electrons can be both particles and waves simultaneously. The downside: these calculations required enormous computing power because they yielded highly detailed descriptions of individual atoms. In other words, if a system with twice as many atoms was simulated, then it would take between twice to four times as much computing power. This was a major problem for simulating systems that involved large molecules and compounds. In a ground breaking move, these scientists were able to focus their simulation on a few of the free electrons or the part of the protein that was most active (Eg. such the active site of the enzyme) and would make a difference in the chemical process. They then used the remaining computing power for less demanding classical physics calculations such as for all other electrons and nuclei involved in the reaction. This new category of simulations was called: QM/MM or quantum mechanics/molecular (or classical) mechanics simulations.
Samia
Hi Samia, That is really fascinating stuff! I am always in awe of folks that have such vision can look at an issue and turn it on its head. With quantum computing, I wonder how this will impact simulation technology? The sky’s the limit, I would think! Thank you for such an engaging reply!!! Dana