One last post!
Good luck everyone with next semester, and congratulations to those who are wrapping MET up!
ETEC 533 – Technology in the Mathematics and Science Classroom
One last post!
Good luck everyone with next semester, and congratulations to those who are wrapping MET up!
Hmmm… I’m not sure if this is a legitimate post for this week so I will likely address the second question later on. Anyway, it seems as though my post from the TGEM week fits nicely into our task requirements. I definitely put some hours into this lesson, so here goes… (the lesson is attached to the end of this post)
Having yet to finish reading the “related literature”, I think I will return with more thoughts to add to my PhET lesson! To be continued!!!!
I’m back! The two papers that I read today were “Reality versus Simulation” and “Fifty Years of Thinking About Visualization and Visualizing in Mathematics Education: A Historical Overview”. ( Srinivasan et al, 2006; Clements, 2014). Relating these reading to my guided inquiry-based, simulation, T-GEM lesson…
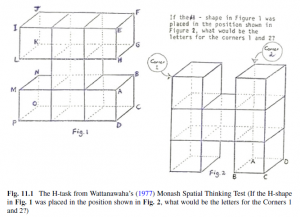
Wattanawaha’s Monash Spatial Thinking Test, (Clements, 2014)
A theme is unquestionably emerging throughout this week’s readings, and linking ideas to previous weeks’ reading, as well. When learning is anchored in real life contexts, students are happier and their construction of knowledge is abundant.
When Third World street vending children are capable of performing complex mathematical processes mentally yet can not perform the same process in a decontextualized problem on paper, how can one not conclude the relevance of situated learning (Carraher & Dias, 1985)? In another study, visitors to a free local museum were interviewed immediately after their trip and two years later. Researchers determined that those visitors whose motivation to attend was curiosity driven, learned more and valued the experience more than those visitors who were merely socially motivated to attend (Falk & Storksdieck, 2009). And when researchers surveyed university biology students regarding their experience using a virtual field trip (VFT), as opposed to a traditional lecture, students overwhelmingly reported positively, 80% of the time, although they also reported that the VFT is best to enhance actual field trips, and not replace them (Spicer & Stratford, 2001).
Each of these readings funnel towards the importance of providing anchored instruction throughout educational practices. I think back to why I enjoyed physics more than any other science and it began with taking Dr. Matthews’ first year physics class where he utilized the entire theatre for his demonstrations and he took incredible measures to draw the most incredible, realistic diagrams. He was also incredibly funny, so I spent most lectures in an amused state! Although his teaching style would still be considered “traditional”, he wove realism into his lectures, every class.
Despite being bombarded with Inquiry Learning approaches in my Professional Development, and with Vygotskian Constructivist Theory in MET, I still believe that in my subject areas, senior physics and academic math, lecturing has its place. I do not have time to allow students to discover Every. Single. Concept. Nor can I allow them to choose what learning outcomes they wish to learn about. My students are future engineers, doctors, and other intensively trained professionals and I am not prepared to sacrifice content for ease and happiness of the learning experience. To students who are not handling the rigour of my courses, I say, it is OK. It is OK to NOT become a doctor. It is OK to NOT become an engineer. If you can’t take the heat, get out and find a training path that does not require you use math or physics at a high level. That still leaves a HEAP of other, very gratifying professions to follow!
Where I have been “converted” is within the lectures themselves. I would not even call what I do, “lectures”, to be honest. Students still write notes, however, the notes are interactively created. With peers, we do numerous reinforcement activities in a non-threatening, collaborative manner. We construct our knowledge at times, but not at others. My goal is to prepare them for university and college, while providing as many hands on or virtual experiences as possible.
On the other hand, I can see that if I were a junior high or middle school teacher, how I would have a very different perspective.
Well, maybe not for math….
For math, foundational skills are critical and need to be automated at some point. This is not only important for senior high math, but for mathematical confidence and mathematical self-esteem. When students don’t know their times tables, for example, it is like they are in my class underwater, using an oxygen tank (their calculator) to breathe. They know that if they don’t have access to their “oxygen”, they will die. Being THAT depend on a tool to survive is not conducive for a healthy learning environment.
However, in science, bring on the “fun” learning! Situate, anchor, inquire, Jasper, WISE, and network those communities every day, as far as I am concerned! What ever it takes to promote a lifelong curiosity in science should be the goal of every junior/middle science teacher out there. Moreover, the world is depending on us to make this come to fruition! We are systematically destroying our environment, becoming 40-year-old-still-living-at-home dependent on technology, and perhaps most shockingly, in astonishingly high numbers, receiving our baseline news from Facebook.
<Please prepare yourself to be “should” on. I don’t like to engage in this practice, but every once in awhile, it needs to be done.>
If we do one thing, as a collective of educators, it should be to teach our younger students how to research, and remain scientifically curious throughout their lives.
That’s it!
Easy peasy.
We’ve got this.
This is a free online, resource for Physics 11 and 12 classes, mostly. Topics include Kinematic Graph Interpretation, Waves, and Polarity, each has an interactive, quantitative and/or qualitative activity for students to investigate. Some work sheets are provided and the authors have recently included a host of interesting videos on a variety of different topics.
Unfortunately, it is possible for students to simply “guess and check” on the simulations until they pass a level. The accompanying worksheets would mitigate this negative outcome, however. I would be inclined to use this site as a reinforcement activity, as opposed to a learning activity, so that as many students as possible would actually use the principles of physics. It would be great if educators could embed questions, in between levels, to check for understanding, as students navigated through levels.
Of the videos that I have seen, they could be used in a Jasper Style or WISE platform as points of discussion and problem solving. They each seem to revolve around a single concept in physics; students could discuss the principles of physics at play in the videos, in a forum on WISE or as a class discussion.
Although this may be better digested by a high school crowd, the metaphor that this instructor uses to simulate space-time is extremely visual. I would LOVE to have this in my classroom one day. In the video, Mr. Burns simulates how masses are gravitationally attracted to each other, why smaller objects orbit larger objects, why the planets are moving in the same direction around the Sun and how the moon can orbit the Earth, whilst also orbiting the Sun. Should someone physically recreate this metaphor in their room, I think that it would satisfy most of, if not all, the requirements for an effective metaphor.
If the Wicked Witch of the West co-authored this week’s reading, it may have been subtitled,
“U’m- Welting!”
I always know when I am enjoying a week more than others, based on the amount of effort I put into the reading and note taking. And without any sarcastic undertones, I can honestly say that this week was a huge time suck. Perhaps it is the “science-geek” in me that really favors learning about theories that are neurologically situated (I’m not a neurologist, and I don’t even play one on TV, but neurological research unquestionably fascinates me). Perhaps it is that I am a self-proclaimed Queen of Analogies. All I know is that this week really blew my hair back! Floated my boat! I really picked up what the authors were laying down! Hopefully, you are reading my mail, here. (OK… I think I’m done now.)
If you did not read, “Understanding Needs Embodiment: A Theory-Guided Reanalysis of the Role of Metaphors and Analogies in Understanding Science” (Neibert, Marsch, & Treagust, 2012), I highly recommend that you save the PDF for recreational reading at a later time. Although you may not profess to be the King, Queen, and/or Joker of Analogies in your classroom, there is no possible way that one can avoid using analogies/metaphors (and yes, there is a difference) within one’s day-to-day speech. The authors provide a simple example such as “I see your point” as a metaphorical representation of understanding and vision. As a teacher in a school with 20% of the population being in our International Program, I am very careful to explain some of our “weird” Canadian sayings— just this week I was explaining the analogy “Six of one and half dozen of the other.”
So what makes a great analogy/metaphor (a/m) versus an ineffective analogy/metaphor?
Questions to chew on:
Looks like I’m past my word count… time to make like a baby and head out!
P.S. In case you were curious…