Monthly Archives: April 2017

For my TELE final project I chose to do an inquiry on plants with my grade 3’s integrating the T-GEM theory. I posted a link to my project in the Student Café and received some awesome feedback from some classmates (thank you!). If you would like to take a look at my project, here is the link: https://etec533.wixsite.com/growplantsgrow

I chose to create a graphic outlining my steps using the T-GEM learning theory.

The virtual lab I would integrate into the generate phase would be this virtual lab on Light and Plant Growth to encourage students to think about possible hypotheses and questions for their own projects.

My fifth and final step is to incorporate a sharing aspect to showcase student learning. With this project the sharing would be in the form of a science fair with information on the project, a display of the plant(s) used, and a food connection sample for visitors to try.

As another technology connection, as Catherine suggested to me, I may also incorporate the creation of a digital story for students to showcase their observations made throughout the project in a creative way. Technology integration is a great way to enhance learning and offers additional ways for students to share and document their learning.

Khan, S. (2007). Model-based inquiries in chemistry. Science Education, 91(6), 877-905.

Khan, S. (2010). New pedagogies for teaching with computer simulations. Journal of Science Education and Technology, 20(3), 215-232.

I have come to recognize that many of my senior math students do not make a connection between transformations and algebraic processes.  They struggle to make the connection between physical movement and algebraic effect.  This activity is intended to assist these students in building connections in this area.

1. Step 1 – Review Cartesian planes and coordinate systems
   1. Access prior knowledge
   2. Identify any misconceptions or gaps in learning that should be addressed in these areas before moving forward.
2. Step 2 – Student Hypothesis
   1. Working in pairs, students will create rules for translations, reflections, and rotations while working with coordinates (e.g. when translating horizontally, the x-coordinate of each point is adjusted accordingly)
   2. While working on developing their hypotheses, students have access to a tabletop grid and shape cutouts to manipulate
3. Step 3 – Test hypothesis
   1. Use Geometer’s Sketchpad to test hypothesis using prescribed “test” transformations
   2. Students access transformations from a list within the Geometer’s Sketchpad file
   3. Transformations will include confounding situations, such as a rotation in the opposite direction or a reflection in something other than an axis.
4. Step 4 – Refine rules/hypothesis in consultation with a small group
   1. Students combine into groups of 3-5 students to discuss findings, inconsistencies, confirmations, etc
   2. Groups come to an agreed upon set of rules by discussing and justifying their perspectives.
5. Step 5 – Use transformation rules to design a patterning activity for other groups in class
   1. Each group will use Geometer’s Sketchpad to design a problem scenario involving transformations that will require other groups to apply their transformation rules.
   2. Examples of problem scenarios could include designing a quilt pattern, wall or floor tiling, yard landscaping, etc. The scenario context will be an essential component of the framing of the application because “contexts allow the learner to reflect on and control for the meaning and reasonableness of their developing ideas” (Dixon, 1997, p. 140).

Dixon, J. K. (1997). Computer use and visualization in students’ construction of reflection and rotation concepts.School Science and Mathematics, 97(7), 352-358.

Elementary Science

Topic: Mass

Misconception: That the size and shape of (an) object(s) affects the balance on a scale even if the weight is the same

Students can sometimes get confused between the type of objects you may put on both sides of a scale and its impact on balance.  Some students think that if you put 1 pound of paper clips on one side of a scale and a 1 pound cube, the scale will not balance out.

Materials:

• Balance scales
• Computers
• Different objects

Lesson:

• Assess students prior knowledge by asking them when using a balance scale, what is the relationship between the length of the arm and the mass of the objects that balance on it? Do different materials impact the balance of the scale?
• Ask students to discuss with a partner how they will be able to get the scale to balance using different materials
• Ask students to come up with a theory for how to get the scale to balance perfectly level
• Ask students to use different materials to place on each side of the balance to see if smaller less heavy objects on one side and a single heavy object on the other of equal weight will influence the balance scale.
• Have students hypothesize and test out if adjusting where the object(s) are placed on the scale influences
• In partners, have the groups come up with some new rules for understanding weight and mass.
• Have students use the PhET “Balancing Act” to test out different materials and their weight. https://phet.colorado.edu/en/simulation/balancing-act

This lesson draws upon the T-GEM model.  According to Khan (2007) this model focuses on three important steps: Generate, Evaluate, and Modify.  In this lesson students are asked to generate their own ideas around mass /weight and how different objects will influence the balance of the scale. The students compare their predictions with their partners and then test out their theories that they have come up with.  After testing their hypothesis various times, the students then come up with some scenarios why different objects and lengths of arms will influence the balance scale. This is the ‘evaluate’ portion of the T-GEM.  The last stage of the lesson allows students to modify their original beliefs about weight and mass.  They are able to gain an new understanding regarding the relation of weight and mass to balance.  The extension part of the lesson is meant to give students further time to experiment with the ideas that they toyed with in the lesson. As Stieff et al (2003) discusses, it’s important to give students opportunities to give students virtually unlimited opportunities to experiment with real world objects.  Using visualizations allows students to understand the differences between physical variables and the equilibrium posting (Stieff et al, 2003). Students have the opportunity to test what they’ve learned  about balance and make predictions about how different objects will make the plank balance.

References:

Khan, S. (2007). Model-based inquiries in chemistry. Science Education, 91(6), 877-905

Stieff, M., & Wilensky, U. (2003). Connected chemistry – Incorporating interactive simulations into the chemistry classroom. Journal of Science Education and Technology, 12(3), 285-302.

Mathematics

Targeted Group:         Grade 7

Format:                       Number Sense and Numeration – Adding Fractions

Misconception:           Adding fractions without finding common denominators or equivalent fractions.

Rationale:

Students have a great deal of difficulty with fractions and understanding why they need a common denominator in order to add them. As this seems to be an issue each year with grade 7 students I thought it would be a good idea to find new ways to address the concept.

Goals:

Students will be able to add fractions competently with like and unlike denominators, finding equivalent fractions in authentic problems.

Materials:                   Virtual fraction manipulatives

http://www.mhhe.com/math/ltbmath/bennett_nelson8e/VMK.html?initManip=fractionBars

Smartboard notebook software – Specific lesson plans
Authentic addition of fractions questions.

Process:                    This can be done individually or in pairs.

Step 1:

Give students a step by step adding fractions task sheet with three different tasks. The step by step process allows the students to see how the common denominator is found and how to add the fractions.

Step 2:

Direct students to the virtual manipulatives at the above URL.  This would be in their Edmodo folder already so they just have to click on the link.

Step 3:

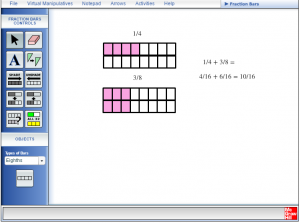
Direct students to create the model shown on the task sheet on the virtual page using fraction blocks. Students should write the addition statements on the virtual page, and then transfer them to their task sheet. They should continue to do this for all the questions on the task sheet.

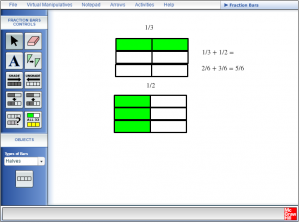
Step 5:

Ask the students to create their own addition problem using the fraction bars for the other students in the class to try. Students should be sure to draw this on their task sheet including the correct addition statements.

Consolidation Activity:            Smartboard Notebook Lesson

Task:

Introduce students to the Land Ownership task. Show them the picture of the land split into various areas for different owners in SmartNotebook. Students can use this software on the laptop computers using the mouse.

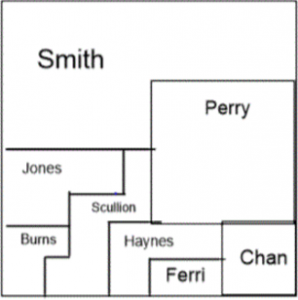
Work with a partner.

The map shows land owned by 8 families.
Determine what fraction of the land each family owns.
Four families sold land to the other four families.
Use the first map clues to help you draw the new map. You can use the back of the sheet to do this.
Write the addition to show each of the transactions.

CLUES

1. When all the sales were finished, four families owned all the land – Smith, Perry, Haynes, and Chan.
2. Each owner can walk on their land without having to cross another person’s property.
3. Smith now owns 1/2 the land.
4. Perry kept 1/2 of her land and sold the other half to Chan.
5. Haynes bought land from two other people. He now owns 3/16 of the land.
6. Chan now owns the same amount of land as Haynes.

Students use the tools in SmartNotebook to colour in the areas owned by each family and manipulate the shapes to find the smallest piece in order to determine the common denominator. Once they have done this, students find the equivalent fractions for each of the owners property showing the fraction in equivalent form and simplest form. For example: Perry = 1/4 or 16/64.

When they have found all the equivalent fractions it should be easier for them to rearrange the fractions for the four families to own all the land according to the clues. They need to show the new configuration on their screen or paper, and show the addition statements that go with their solutions.

Education Theories:

The educational theories that are associated with this lesson plan are Learning for Use and Anchored Instruction.

Learning for Use framework is a pedagogical framework that integrates the content with the processes of the subject matter. Using the virtual manipulatives allows the students to visualize the process of creating the equivalent fractions, how a common denominator is determined, and then how the two fractions are added together. Since the content is being able to add fractions with unlike denominators, the manipulatives allow the students to try a lot of different combinations of fractions to find their equivalents and add them. The virtual manipulatives also allow the students to discover these concepts for themselves, and build upon that understanding using the tiles to create a number of different combinations.

Anchored instruction is the process of presenting instruction in the context of an authentic environment with problems or issues which learners must resolve. The problems or issues which are presented to learners in the authentic environment are “anchors” which link learning of content and skills to authentic tasks and activities in which the learning must be used (Gittens, Thompson, & Carter).  Although this is not a true representation of anchored instruction, the concept of buying and selling parcels of land is a real world connection. It is difficult to find authentic problems using fractions that the students would recognize. This problem could be related to their history or geography lessons particularly with New France and Seigneurial Systems or land use changes.

Using the virtual manipulatives aids the students in consolidating their understanding of equivalent fractions and common denominators, then transfer that understanding to a different task, using a different medium which demonstrates their understanding in environments other than those directly related to the specific learning environment (Dixon). Using a variety of mediums (virtual manipulatives, Smartboard tools, pencil and paper) students can consolidate their knowledge using anchored instruction and specific technology to augment their knowledge and increase their conceptual understanding.

Anne

References:

Dixon, Juli K, 1997. Computer use and visualization in students’ construction of reflection and rotation concepts. School Science and Mathematics, Volume 97(7), University of Nevada, Las Vegas.

Kathy-Ann Daniel-Gittens , Kelvin Thompson and Philip Carter (2014). Anchored instruction. In K. Thompson and B. Chen (Eds.), Teaching Online Pedagogical Repository. Orlando, FL: University of Central Florida Center for Distributed Learning. Retrieved April 3, 2017 from https://topr.online.ucf.edu/index.php?title=Anchored_instruction&oldid=3577

One of the major advantages to using digital simulation is the ability to aid students in visualising the invisible.  In the Science 10 unit, balancing chemical equations is something that many of my students have had difficulty with.  In the past, I have always fallen back on drawing and counting molecules before transitioning to more abstract calculating of number of atoms when helping students.  But the process of balancing chemical equations also lends itself to a T-GEM process using PhET simulations that both help students understand the process with analogies and also to provide them a visual reference of the atoms.  Moore, Chamberlain, Parson, & Perkins (2014) found benefits in using simulations in chemistry classes, noting that “students can engage with and discuss dynamic systems that provide feedback specifically designed to support student learning.”  This fits neatly with the T-GEM process which plans a series of lessons that support individual learning by encouraging students to explore scientific concepts and generate theories about their relationships, then evaluate their newly constructed knowledge, and finally modify their knowledge based on the feedback from their evaluation. (Khan, 2007)

The lessons utilize three PhET simulations to start students on the concept of balancing, analogies of balanced processes, and finally the act of balancing chemical equations.

Lesson 1: Initiate Ideas – Balancing Simulation (Balance Lab)

The goal of this lesson is to prime students on the concepts of balancing.  While the simulation is not strictly related to chemistry, it does visually demonstrate the concept of two parts of a single system being in balance.  This will be revisited in a few lessons when students are to balance reactants and products in a chemical equation.  In addition, it will serve as a starting point of a brainstorm/discussion on what other common everyday events require “balancing” and the beginning and end of the process have some quantifiable link.

Lesson 2: Generating A Theory – Reactants & Products (First with Sandwiches, then with Molecules); Additional activity – Law of Conservation of Mass Undemo

The next lesson will take the concepts of balancing and start to connect them with chemistry concepts.  In particular, the simulation allows students to change the number of sandwich ingredients (reactants) and see the number of complete sandwiches (products) that can be made.  During this activity, the discussion will lead towards the ideas of the ratio of reactants to products.  Once students feel they have a grasp of the sandwich analogy, they can move to the molecule simulation to transfer their thinking to atoms and molecules.  In addition, a live demonstration of the Law of Conservation of Mass using chemical reactants will be shown and, using the results from all three activities, students will start to formulate for themselves a concept of balanced chemical reactions.

Lesson 3: Evaluating Their Knowledge – Intro to Balancing (Introduction activity only)

As a way of evaluating their knowledge, the students will balance the three chemical equations provided in the Introduction activity.  For each equation, they will first predict the adjustments necessary to balance the chemical equation.  They are encouraged to using the knowledge generated from the lesson prior to complete the equations.  After their prediction, they can explore both visualization tools (scale and bar graph) as well as the actual molecular diagrams as they adjust the number of each molecule to balance the equations.  As part of their individualized learning, they are encourage to pick one of the three visualisation methods to use regularly.  The class will finish with a sharing of various balancing strategies in order to highlight general processes used to tackle the problems.

Lesson 4: Modify Their Knowledge – Continue with Balancing (Game activity)

The Game activity has 3 difficulty levels, each with 5 questions.  The students are to work through all 15 questions from Level 1-1 to Level 3-5, utilizing the strategy from Lesson 3.  They are free to choose whether they want their attempts to be timed or not as a personal challenge.  During this process, the teacher should be circulating and guiding students as they work through these problems, helping them re-formulate their processes as necessary if they answer a question incorrectly.

Lesson 5: Extension Of Knowledge – Working with Balanced Equations (Game activity)

The Reactants & Products simulation from Lesson 2 has a Game activity that can be used to assess and challenge student understanding.  The Game provides students with a balanced equation and a specific number of either reactants or products.  Using the ratio given in the balanced equation, the students have to determine the number of molecules required to complete the equation.  This will challenge students to consider balanced equations from a different perspective from Lesson 4.  Student understanding can be assessed formatively by engaging in discussion with them as they answer the 15 challenge questions.

References

Khan, S. (2007). Model-based inquiries in chemistry. Science Education, 91(6), 877-905.

Moore, E.B., Chamberlain, J.M., Parson, R., Perkins, K.K. (2014). PhET Interactive Simulations: Transformative Tools for Teaching Chemistry. Journal of Chemical Education, 91(8), 1191-1197

Background:

Financial literacy is highlighted throughout the elementary grade levels in the Content area of BC’s New Curriculum. Most paper-pencil curricula address money identification, counting coin and dollar amounts, and one or two step word problems connected to money. However, these paper-pencil activities minimally equip students for financial literacy skills and applications. While exploring the information visualization simulators during this past week, the elementary and middle school simulations from Illuminations were easy to understand and seemed quite plausible to implement into already developed curriculum.

Literature Support for Lesson Cornerstones:

In a study conducted by Srinivasan, Pérez, Palmer, Brooks, Wilson and Fowler (2006), engineering freshman students who completed learning using MATLAB did not experience what they perceive as an authentic experience. The students felt that their experience was disconnected from real expert experience because they manipulated a simulated system rather than a real-life system. The researchers conclude that a probable reason for this disconnect is that the students “need/want authenticity to be able to make connections the experts make with the simulation” (Srinivasan, 2006, p.140).  This perception from the students leads educators to consider the value of real-life experiences in connection with simulated experiences.

Transferring simulated experiences to real-life experiences is supported through the study completed by Finkelstein, Adams, Keller, Kohl, Perkins, Podolefsky and Reid (2005). In their study, students in a second semester introductory physics course, who had used a simulation first to design a circuit system, were more successful later in designing real-life models. These same students also achieved greater success on related exam material that was completed two months after the simulated and real-life circuit building experience (Finkelstein, 2005). Due to these findings, authenticity of learning through the transferring of knowledge from simulation to real-life experience is a main cornerstone of the following lesson design.

In addition to authenticity, two lesser cornerstones, rich content and goal challenge motivation, are also incorporated into the lesson design as supported through the writings of Srinivasan et al. (2006). A pre-test assessment begins the lesson in order to determine prior knowledge and the optimal area of learning for the individual student. As well, this pre-test assessment can be used to determine pairings/groupings throughout the lesson activities. By providing rich content within the lesson plan, this affords opportunity for students with less prior knowledge to acquire new knowledge before exploring the simulated and real-life experiences. Building prior knowledge within students is critical for their success as Srinivasan et al. (2006) state, “Prior knowledge accounts for the largest amount of variance when predicting the likelihood of success with learning new material” (p.138). In regards to gaining knowledge of the student’s optimal area of learning, this connects closely to Vygotsky’s zone of proximal development, but is also supported by goal oriented motivation when learning goals are neither too steep, nor too simple: “If learning goals are too steep for a learner’s current context, learning is not successful. On the other hand, when learning is simple for the learner, the instruction can become over-designed and lead to diminished performance” (Srinivasan, 2006, p. 139).

Lesson Overview:

The following lesson incorporates the instructional framework of anchored instruction. This has been accomplished through a narrative multi-step problem solving feature. The three cornerstones highlighted in the section above are evident within the lesson: goal challenge motivation {decided by pre-test assessment}, content-rich material, and authenticity through real-life application.

LESSON

Pre-test Assessment:

Provide paper-pencil assessment including photos of Canadian coins asking students to identify individual coins.

Addition questions for pre-test assessment may include:

• How many quarters makes a dollar? How many dimes? How many nickels?
• Show 3 different ways of making one dollar using a mix of coin types. Draw coins with labelled amounts to share learning.

 Include two ‘making change’ questions that require student to calculate amount of change from $1.

Content-rich Material:

Read and discuss Dave Ramsay’s book entitled, My Fantastic Fieldtrip on saving money.

Provide pairs of students with real sets of Canadian coins with accompanying anchored money solving problems. Problems may require students to interact with other students in the class or with the teacher. An example of an anchored money problem solving scenario follows:

Macey has been saving her allowance for seven weeks. She has a saving goal of $20.00. Each week she receives $1.50. Three weeks ago, Macey decided to buy her sister a rubber ball for her birthday which cost $1.00.  She used a loony from her savings . After seven weeks, Macey wanted to exchange all of her quarters for loonies, but she also wanted to keep half a dozen quarters for when she visited the candy machine at the grocery store when she went shopping with her mom.  She knew that several of her classmates had loonies that they could exchange for her quarters. (At this time, go around to your classmates and exchange your quarters for loonies just like Macey wanted to.) Once Macey exchanged her quarters for loonies with her classmates, how many loonies does Macey have? How much money does Macey have all together? How much more money will Macey need to save to reach her saving goal?

Simulation  Activity:

Illuminations –  Coin Box {elementary level}: Initially, direct instruction is required to demonstrate how by clicking on the cent icon in the bottom right corner, the student can see the amount of each coin as they are  US coins and difficult to decipher visually. Direct instruction should also be provided to guide the student to the “Instructions” tab and show the subtitled areas “Modes”. Student can then have time exploring the “Activity” section using the dropdown menu in the top left corner. Student should have ample time to explore all five activities including: “Count”, “Collect”, “Exchange”, “Change from Coins”, and “Change from Value”.

Transfer to ‘Real-Life’ Context: Students should have opportunity to transfer the simulated learning to a real-life context. An example of a real-life context is provided below, however adapting this to uniqueness of the learning community is recommended:

Cookie Sale –  Each student bakes one dozen cookies to sell to classmates and other students at the school. Pricing: 1 cookie = $0.40, 2 cookies = $0.75, 3 cookies = $1.00, 4 cookies = $1.25, 5 cookies = $1.45, 6 cookies = $1.70. This activity allows for assessment by the teacher through observation. Student’s accuracy and ease of providing change could be assessed using a simple checklist. Students should work in pairs  or small groups to help ensure that change to buyer is accurate.

Self Assessment/Reflection: A reflection activity is to be completed by each student. This activity requires the student to reflect on and share about growth and relevancy of learning. A self assessment printable is here:

Self Assessment

Finkelstein, N.D., Perkins, K.K., Adams, W., Kohl, P., Podolefsky, N., & Reid, S. (2005). When learning about the real world is better done virtually: A study of substituting computer simulations for laboratory equipment. Physics Education Research,1(1), 1-8.

Srinivasan, S., Pérez, L.C., Palmer, R.D., Brooks, D.W., Wilson, K., & Fowler, D. (2006). Reality versus simulation. Journal of Science Education and Technology, 15(2), 137-141. doi: 10.1007/sl0956-006-9007-5