Category Archives: B. T-GEM

A challenging Chemistry concept is explaining periodic trends, connecting related concepts of radii, ionization energy, electronegativity, electron affinity and melting point. Although data booklets provide empirical values, learners not only fail to appreciate how much work is done by the scientific community over lengthy periods for each point (Khan, 2010), they resort to memorizing trends with little understanding. For example, on practice tests students explain why Fluorine has the highest ionization energy because it is most electronegative (both of which are effects of underlying principles of effective nuclear charge and radii). On explaining radii, they state Fluorine is smallest because atoms get smaller towards the top right corner of the periodic table. Possible misconceptions arise given the order of magnitude in picometers, abstractly described at sizes too small to visualize. Similarities in definitions between ionization energy and electron affinity (and later electronegativity) make learning trends challenging as students attempt to understand key concepts while expected to compare different elements given periodic table arrangement.

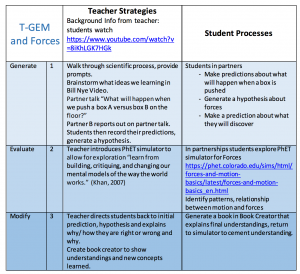
A possible T-GEM Cycle might be as follows:

Generate: Define atomic radii and ionization energy so learners have rough idea of what data represent

Evaluate: Present radii data for an individual row (ex. Li to Ne) asking students to find trend between radii and atomic number. A possible conclusions is that atomic radii decreases with more protons, graphing element radii versus atomic number.

Modify: Have students compare whether pattern works for other rows on the periodic table (ex. Na to Ar). Identify discrepancies like: Why is Na bigger than Ne (reviewing number of shells), and Why is Ne bigger than F (introducing electron repulsion).

Evaluate: Present ionization energies for individual periods, asking students to find trend between IE and atomic number. A possible conclusion is that ionization becomes harder with more protons, graphing IE versus atomic number.

Modify: Have students compare whether pattern works for other periods. Identify discrepancies like: Why does Na have lower ionization energy than Ne (reviewing number of shells), and Why is O’s electron harder to remove than N (introducing half filled p stability). Learners can extend trends comparing ionization against radii.

A possible technology contribution would be the ‘Periodic Table’ Chemland simulation: http://employees.oneonta.edu/viningwj/sims/periodic_table.html

Clicking ‘Relative Radius Covalent’, displays relative element radii as bar graphs arranged on the periodic table, using visuals to make sense of raw data. Learners can similarly click ‘Relative Energy First Ionization’ to test whether their discovered patterns are empirically consistent or whether theoretical models need to be reorganized.

*For my final TELE design, I am considering addressing similar concepts but primarily using Excel to graph data to make visual sense of patterns in the data booklet. Compiling information for atomic number, radii, first ionization, electron affinity, electronegativity and melting points, students can identify patterns across individual rows and columns, presenting discrepant events to have students iteratively refine models.

References

Khan, S. (2010). New pedagogies for teaching with computer simulations. Journal of Science Education and Technology, 20(3), 215-232.

The BC Science Curriculum for grade 4 includes the Big Idea of “The motions of Earth and the moon cause observable patterns that affect living and non-living things”. To investigate the challenging concept of changing tides as it affects living and non-living things on Earth (due to Earth’s axis, rotation, orbit around the sun, gravitational pull of the Moon and lunar phases), the T-GEM model will be used to support student inquiry using tidal simulations and teacher guided strategies. In the T-GEM model, Khan emphasizes the importance of teacher actions that promote student inquiry (Khan, S., 2010), therefore, teacher guidance, as to when to use the technology throughout the process, is key to students generating relationships and evaluating patterns effectively in the creation and modification of their mental models.

Often, tides due to gravitational pull is a difficult concept for students, as it requires them to create an accurate scientific mental model of the role of the Sun, the Earth’s axis and the Earth’s orbit, which are not directly observable phenomena for students. The enhancement of a digital simulation, in conjunction with the cyclical Generate (G), Evaluate (E) and Modify (M) model should help enrich students’ involvement and engagement with scientific inquiry and provide opportunities to build accurate mental models of unobservable phenomena (Khan, S., 2007).

Technology Links:

Technology Links for T-GEM: Tides

References:

Khan, S. (2007). Model-based inquiries in chemistry. Science Education, 91(6), 877-905.

Khan, S. (2010). New pedagogies for teaching with computer simulations. Journal of Science Education and Technology, 20(3), 215-232.

To launch the beginning of our units of inquiry in Grade 5, we begin by exploring the big idea of Multicellular organisms have organ systems that enable them to survive and interact within their environment. Before students begin to piece each system together, to understand the interrelatedness we explore each system in isolation, while providing opportunities for students to write and generate questions when hypothesis to connections occur. Students participate in the inquiry cycle by finding out, sorting out, making connections to information. When exploring the form and function of the circulatory system, and the human heart, many students struggle with understanding how oxygenated blood is transported throughout the body, and in particular are often confused by the use of blue blood on models to represent deoxygenated blood. The following 3-Step T-GEM cycle is included below to explain how digital technology supports student understanding.

GENERATE

During the first phase of the T-Gem Model the teacher provides opportunities for the students to express their understanding. Students are given a blank model of the human body to record their knowledge and predictions of the circulatory system, including veins and the heart. Students then watch the Brainpop video on the Circulatory System to record additional information.

Students generate ideas about what they know regarding the circulatory system by labelling the blank human body template. Students then have opportunity to share their ideas in a gallery walk first, then in small groups of 3-4 students. Students discuss, compare, and explain concepts and questions.

EVALUATE

After watching the brainpop video on the circulatory system, as well as investigating the heart and circulatory through the Heart | 3D Atlas of Anatomy app allow to spin a highly realistic 3D heart model as it was in user hands.

As a class, we discuss our initial predictions and human body diagrams.

Working in small groups of 2, students evaluate what they now know about the circulatory system. Teacher circulates and provides an opportunity to discuss and guide student inquiry. Opportunities for the GEM cycle occur.

MODIFY

After exploring the videos, working through the 3D Atlas of Anatomy apps, including the dissection options, as well as class discussions, students are then able to go back and sort out their new knowledge by redoing their human body template.

Students redo their human body template based on discussions with the teacher and classmates. As an extension, students can work with the EdTech teacher using the 3D school printer to create their own model of the human heart. Students complete a reflection piece to solidify their learning journey, accounting for all growth in understanding.

References

Khan, S. (2007). Model-based inquiries in chemistry. Science Education, 91(6), 877-905.

Khan, S. (2010). New pedagogies for teaching with computer simulations. Journal of Science Education and Technology, 20(3), 215-232.
Khan, S. (2012). A Hidden GEM: A pedagogical approach to using technology to teach global warming. The Science Teacher, 79(8). This article was written about T-GEM with middle-schoolers.

In Physics 11 the concept of torque is often quite easy to calculate but, from my experience, is not something that many students fully understand.  The implications of torque are enormous in engineering but also have real world applications for our students.  Many of our students have been on a ‘teeter-totter’ and experienced the effects of leaning back to go down faster.  I would present students with the problem of a loaded bench press (4-45lbs plates a side) and ask their thoughts on how many plates I can take off one side before the bar flips.  The intention of using this example is it would relate to my students and would have them think about torque in their daily lives.

I would use the following question to guide the inquiry process:

How can we explain the gym using physics? What is the safest design of a bench press to prevent weight tipping?

The question is intentionally broad as there is no single answer to it.  We will approach it through the lens of torque (and can revisit from other angles as we see fit – pulleys etc).

Any thoughts or suggestions on the design process or the guiding questions?

Baljeet

Khan, S. (2007). Model-based inquiries in chemistry. Science Education, 91(6), 877-905.

Khan, S. (2010). New pedagogies for teaching with computer simulations. Journal of Science Education and Technology, 20(3), 215-232.

In Grade 5 science we learn about forces and how they multiply or change direction. Students easily understand that something makes it hard to push a box across the floor but the idea of different forces changing the effect is hard as the forces are not visible. Through the use of the PhET simulator students are able to interact with different forces and as Khan identifies “[i]n dynamic situations, mental models can be manipulated and transformed on the fly through simulation and provide predictive and explanatory power for making sense of the familiar and the unfamiliar.” (Khan, 2007, p 879)

Sorry the image is so small, but if you click on link below you can see it in a readable size:)

T-Gem Image

References:
“Building Student Success – BC’s New Curriculum.” Curriculum.gov.bc.ca. N.p., 2017. Web. 9 July 2017.
“‪Forces And Motion: Basics‬ 2.1.4.” Phet.colorado.edu. N.p., 2017. Web. 9 July 2017.
“Force And Motion – Bill Nye Clip.” YouTube. N.p., 2017. Web. 9 July 2017.
Khan, S. (2007). Model-based inquiries in chemistry. Science Education, 91(6), 877-905.

Grade 8 Math: Pythagorean Theorem

 One of the challenges I have encountered when teaching mathematics to Grade 8 students is their understanding of the Pythagorean Theorem. They are able to quickly memorize the “equation” but struggle with the conceptual understanding of the theorem. I have noticed that when students are given an equation they can usually solve it, but when given concrete objects or visuals they struggle. They also have the misconceptions that the Pythagorean Theorem applies to all triangles, and that the longest side of all triangles is the hypotenuse. I want to move students from general memorization to conceptual understanding.

B.C. Math 8 Content (2015):

Sorry for the small visual: details are below….

3 step T-GEM:

Generating:

Explain that we are going to be discovering the Pythagorean Theorem. As a class, generate ideas about properties of squares (area, angles, special properties, side lengths, etc.), by accessing students’ prior knowledge – things that the students have been learning about over the years. I want them to make connections to what they already know and prime them for the new information to come. Have them work back – if you know the area of a square, how can you find the side length of that square? Have them generate ideas around this basic concept in partners and then share out. Explore the idea of square root.

Show students a visual of a right triangle. Ask students to speak to different properties of this right triangle. Attend to any new vocabulary (legs, hypotenuse).

Share short Water Demo to get students interested: https://www.youtube.com/watch?v=CAkMUdeB06o

Ask class to give feedback on video. What did they notice?

Evaluating:

 Teacher asks students to discover and then investigate properties of right triangle and the Pythagorean Theorem. Students will use Gizmos (explorelearning.com – account required) computer simulation to further explore the Pythagorean Theorem. Students are able to “manipulate the model to view how it behaves under various conditions, and the outcome of these changes are made visible…” (Khan, 2010, p. 216). Student understanding is documented and shared with the teacher through this program.

Modifying:

Students will summarize and reflect on their understanding and apply this understanding in a different scenario. In a Makerspace or Woodwork setting have students apply the Pythagorean Theorem through carpentry (3-4-5 Rule) or mapping or canoeing activity from a First Peoples perspective (FNESC, 2008).

References

British Columbia Ministry of Education (2015). Mathematics 8. Retrieved from https://curriculum.gov.bc.ca/curriculum/mathematics/8

First Nations Education Steering Committee – FNESC (2008). Teaching Mathematics in a First Peoples Context: Grades 8 & 9. Retrieved from  https://teachbcdb.bctf.ca/download/271?filename=math-first-peoples-mapping-and-transportation.pdf

Khan, S. (2010). New pedagogies for teaching with computer simulations. Journal of Science Education and Technology, 20(3), 215-232.

SaveSave

Noticing the effects of air resistance is easy.  Predicting the effects of air resistance on the motion of an object, however, is mathematically complex and beyond the scope of high school.  In Physics 11, students are introduced to motion without the effects of an atmosphere to keep it simple but highly unrealistic (especially for really fast things like bullets or rockets).  After years, my question is why even bother?  The students effectively learn that physics is only true in books and exams which only solidifies the separation between their informal and formal learning. Empirical tools can do an excellent job of modelling real motion of particles in an atmosphere while also introducing authentic challenges in science, which is more compelling for students (CTGV, 1992a).  The partial sacrifice is the simple analytical math part of the model.

The diagram below summarizes a T-GEM approach to a Compressed Air Rocketry project in which students are given the challenge of designing a rocket that will fly as far as possible on a short blast of air.

The project incorporates the affordances of social learning and making learning visible (Linn, 2003).  Students work iteratively in teams, making their learning visible through diagrams, group meetings, and presentations.  Three e-learning resources are needed for this:

1)  a camera with 60 fps or higher (most phones and all iPads)
2)  access to PhET Projectile Motion online simulator  https://phet.colorado.edu/sims/projectile-motion/projectile-motion_en.html
3)  Access to the freeware program Physics Tracker http://physlets.org/tracker/

Special attention should be paid to helping the students collect quality data, where scaffolding is necessary, or the evaluation part of the activity will collapse. Rich scientific data collection is not a teenage instinct!  On that note, Khan’s study references “experienced science teachers” so often that I am left wondering–is it implied that T-GEM as a framework is difficult to wield without appropriate experience or deep grounding in TPACK?

Cognition and Technology Group at Vanderbilt (1992a). The Jasper experiment: An exploration of issues in learning and instructional design. Educational Technology, Research and Development, 40(1), 65-80

Khan, S. (2007). Model-based inquiries in chemistry. Science Education, 91(6), 877-905.

Khan, S. (2010). New pedagogies for teaching with computer simulations. Journal of Science Education and Technology, 20(3), 215-232.

Linn, M., Clark, D., & Slotta, J. (2003). Wise design for knowledge integration. Science Education, 87(4), 517-538.

In grade 2, a challenging concept for students is ‘forces influence the motion of an object’. This is a Big Idea in BC’s new curriculum for grade 2 (BC Ministry of Education, 2015). Through observations, experiments, and evidence of student learning, it is clear that many students struggle with the concept of force and motion because they hold faulty beliefs derived from living in a world where unseen frictional forces operate (White, 1983). For example, in a grade 2 unit we learned about ‘push and pull’, specifically how force always occurs in pairs, Newton’s third law. After many lessons, videos, and examples, one student came to me and said, “If I push a door open, it’s pushing me with the same force? How can a door push me?”

A digital technology that can work to improve this concept is STEAM, an app that teaches the basics of force and motion. The app uses simulation to help students investigate force and how it affects motion. Students can use the simulation to work through the main concepts with 4 different interactive lessons. I would like to use this next year with my grade 2’s in partnerships. (http://www.teachthought.com/the-future-of-learning/technology/steam-app-forces-motion-simulation/).

In my design of a 3-step T-GEM cycle for this concept, I wanted to include student observations and investigations on force and motion, as well as iPad use with the STEAM app for digital experiments.

Generate:

I would have students use a KWL chart (Know, Wonder, Learn) to fill out what they already know, or think they know about force and motion. Then I would have them compare in small groups. This will be used as an assessment tool for me as well to see what their pre-existing beliefs are, as well as to see the growth in their learning at the end of the unit. As a class we will watch the introduction Brain Pop Jr videos to force and motion. Students will share what they think the relationship is between force and motion. In partnerships, students will predict, compare, and explain different examples of force in a hands-on activity.

Video from BrainPopJr. https://jr.brainpop.com/science/forces/pushesandpulls/

Evaluating:

Students will test their predictions in a hands-on activity. Students will use the STEAM app to investigate force and motion. Students will compare their predictions and observations after both hands-on experiments and virtual experiments. Students will come up with “I wonder” questions to help further guide their inquiry. As a class, we will work through a number of picture books to reinforce the concept of force and motion, as well as incorporate different visual videos. Computer simulations enhance concepts and allow students and teachers the opportunity to view visual representation  in more concrete ways which may lead to more accurate conceptual understandings (Khan, 2011).

Students will take pictures of their experiments to later document in Book Creator.

Modifying:

Students will use Book Creator app on the iPads to reflect on their observations, taking into consideration their original predictions. Students will share their books with the rest of the class. As a full class we will discuss their observations, ideas, and further questions. Structured inquiries will occur to help guide and prevent any misconceptions surrounding the concept of force and motion to answer any “wonder” questions that were not answered.

References:

Khan, S. (2007). Model-based inquiries in chemistry. Science Education, 91(6), 877-905

Khan, S. (2010). New pedagogies for teaching with computer simulations. Journal of Science Education and Technology, 20(3), 215-232.

White, B. Y. (1983). Sources of difficulty in understanding Newtonian dynamics. Cognitive Science, 7(1), 41-65. Doi: 10.1016/S0364-0213(83)80017-2

One challenge for students is to understand the refraction of light.  For example, when a student observes a straw in a glass of water, the straw looks like it is bending. This is due to the properties of light, but this understanding can be fraught with misconceptions regarding how light behaves. Some interesting misconceptions about light may be that water does not reflect or absorb light but light can go through it, light always passes straight through transparent objects (without changing direction) or that light needs air to travel (Sampson & Schleigh, 2016).

Research notes that although light is an everyday phenomenon that we constantly observe, students often display learning difficulties and hold unscientific understanding on physics concepts of light wave (Srisawadi & Kroothkeaw, 2014). In addition, concepts of light such as its speed and wave length are removed from the range of perceptions of the human senses, and so optics instruction can be subject to interpretation, so there is a need for careful consideration in physics teaching process (Srisawadi & Kroothkeaw, 2014). Computer simulations can broach this divide. As noted, computer simulations can enhance generating relationships and allow students and teachers the opportunity to view trends, variables and visual representation  in more concrete ways which may lead to more accurate conceptual understandings (Khan, 2011).

In order to generate information about this phenomenon the educator can begin an open-ended discussion to find out current concepts about light. Questions such as:

What is light?

Where do you think light comes from?

How does light travel?

This will allow the educator to begin to understand what conceptions and misconceptions the students may hold about light and will also allow the students to begin thinking about the concept. As this discussion is occurring the educator can note responses on chart paper or interactive whiteboard so that ideas can be reviewed as the process of understanding continues. As an educator I would incorporate “accountable talk” which will allow students to defend their ideas and question others about their understandings. Examples of accountable talk would be statements like;

“I wonder why….?

“I see what you are saying (rephrase)”

“What you said made me think….”

Then as an educator I would facilitate a review of the ideas generated in the group discussion through referring and restating the list created by students. I would break this down further into “Our First Ideas about Light” and then create another section for questions we now have about light. This would be labelled “Our Questions about Light”. We would brainstorm some questions that we have. Then I would provide students with appropriate books and internet resources about light. I would also show them a model or a picture of a straw in a glass of water. The straw appears to bend and so I would ask them how they would explain the phenomenon. After they have a chance to read/view this information, I would ask them to work with a partner, independently or in a small group (provide choice) and to draw or create a clay model of their understanding of light.

We would then reconvene and compare our models. I would give students time to explain their models to their peers so that I could continue to assess possible misconceptions. At this point the students may begin to reformulate their understandings based on new learning from their peers. Then we would watch several simulations about light refraction. I would ask the students to consider their previous understandings by asking “Do you need to change your original drawing/model? Or “Do you think you need to modify your original drawing/model?”  Our new understanding would be discussed and a new category would be added to our discussion titled “New Understandings”.

Bending Light Simulations

Refraction in Water Simulation

Bending Light Simulation

References

Bending Light. (n.d) Retrieved March 1, 2017, from https://phet.colorado.edu/sims/html/bending-light/latest/bending-light_en.html

Khan, Samia (2011).  New pedagogies on teaching science with computer simulations. Journal of Science Education and Technology 20, 3 pp. 215-232.

Refraction in water. (n.d.) Retrieved February 29, 2017, from https://www.khanacademy.org/science/physics/geometric-optics/reflection-refraction/v/refraction-in-water

Sampson, V., & Schleigh, S. (2016). Scientific Argumentation in Biology [PDF file]. Arlington,Virginia. NSTA Press Book. Retrieved from  http://static.nsta.org/files/PB304Xweb.pdf

Srisawasdi, N. & Kroothkeaw, Supporting students’ conceptual development of light refraction by simulation-based open inquiry with dual-situated learning model. S. J. Comput. Educ. (2014) 1: 49. doi:10.1007/s40692-014-0005-y

Initially, I found it challenging to apply T-GEM to mathematics as I found it hard to picture, but after completing this activity, it seems to be very similar to many of the activities I already strive to do with my students.  A challenging concept for my students in secondary math is creating and understanding equations for lines and quadratic polynomials using graphs or scenario details.  This challenge has been identified through concept pre-assessments, the nature of their questions throughout their work, and continued struggles on summative assessments.  They struggle to make the connection between the information they are given and the algebraic, abstract representation.

Generating: For the generating phase, I would have students brainstorm what they already think they know about equations with regards to what they mean and how they can be used.  Students will randomly select equations from a centralized equation bank to explore using Desmos (available either online or as an app).  Working in pairs, students will develop a set of rules for creating equations based on their explorations of manipulating equations within Desmos.

Evaluating: Once students have developed their guidelines, pairs of pairs will be joined into groups of 4, in which students will compare their initial hypotheses and justify their perspectives.  Ideally, reflection would occur as students need to explain how they arrived at particular conclusions. At this point, scenario-based problems will be introduced to the original pairs, expanding upon the initial work with base equations.  Students now need to determine if the rules they established in their initial phases apply appropriately to their new scenarios.  If they are not able to use their rules to accurately create an equation to represent the scenario and use it to solve problems, they will need to identify the gaps and determine what adjustments need to be made.  Desmos will continue to be the technology tool at this level, as students are able to easily test, adjust, and visualize their inputs.

Modifying: In their pairs, students will reevaluate their list of rules for equations, taking into consideration their initial hypotheses, their discussions with peers, and their testing of their hypotheses.  As a class, we would come back together for a large class discussion to compile their ideas into a community-based understanding.

This process could be further expanded to include different types of polynomials.  For example, students initially working with equations of lines could then generate, evaluate, and modify new hypotheses regarding quadratics, based on their work with linear relationships.  Subsequently, work with quadratics could be further cycled to work with cubics, then quartics and other higher order polynomials, as appropriate.

By having students use Desmos to work with the different parameters of the equations, they are able to actually experiment to see the effects of changes, rather than simply being told to memorize, for example,  that the c value of a quadratic equation determines the vertical position of the graph but doesn’t directly affect its shape when a and b stay constant.

I believe that many mathematical principles and concepts can be approached using similar strategies to those used for scientific principles and concepts, and aim to include them when possible in my teaching.  One challenge I have in senior math is the perception of teachers regarding the comparable value of experimentation and hands-on math in the university-bound courses as compared to the middle school or college/workplace-bound courses.  I am often met with resistance from colleagues who don’t believe there is a place for experimental or hands-on learning in the higher-level university-bound courses, and that such activities are frivolous at that level. Do you feel that there is value in hands-on math learning for the senior level university-bound math students?

Sources Consulted:

Khan, S. (2007). Model-based inquiries in chemistry. Science Education, 91(6), 877-905

Khan, S. (2010). New pedagogies for teaching with computer simulations. Journal of Science Education and Technology, 20(3), 215-232.